A common user complain about OWL DL is that it does not support metamodeling, which allows one to describe additional level(s) of classes and properties. In order to make use of (decidable) ontology reasoning, users has to restrict themselves into OWL DL. In practice, it is often not realistic to ask users to transfer their ontologies with meta-classes and meta-properties into ones without. Although OWL Full provides some metamodeling; however, it is not decidable. It has been pointed out that if we just ignore the need for metamodeling, some users will simply not use OWL, and the whole effort could become a failure [3].
Motik [1] proposes two alternative metamodeling approaches for OWL, i.e., the context approach and the HiLog approach. In the context approach, metamodeling is provided by allowing that the names for classes, properties and individuals are not distinguished from each other. The trick is to provide them different interpretation functions according to the context. Consequently, the interpretations of a class and an object sharing the same name are completely independent, which leads to non-intuitive result. For example, in this approach, if two objects teacher and lecture are asserted to be equivalent, the interpretation of the class teacher can be an empty set, while that of the class lecture can contain some objects, such as Frank. In the HiLog approach, the semantics is more intuitive; however, existing DL reasoners can not be reused, and one has to implement new reasoners.
This paper proposes OWL FA, an extension of OWL DL with the metamodeling architecture of RDFS(FA) [2]. There are two nice features of OWL FA. Firstly, it is a decidable extension of OWL DL. Secondly, the knowledge base satisfiability problem of OWl FA can be reduced to that of OWL DL, which indicates we can reuse existing DL reasoners to support OWL FA.
Intuitively, OWL FA introduces a stratum number in class
constructors and axioms to indicate the strata they belong to.
Let i ![]() be an integer.
OWL FA consists of an alphabet of distinct class names i
(for stratum i), datatype names , abstract property names
i (for stratum i), datatype property names and
individual (object) names (); together with a set of
constructors (with subscriptions) to construct class and property
descriptions (also called OWL FA-classes and
OWL FA-properties, respectively).
be an integer.
OWL FA consists of an alphabet of distinct class names i
(for stratum i), datatype names , abstract property names
i (for stratum i), datatype property names and
individual (object) names (); together with a set of
constructors (with subscriptions) to construct class and property
descriptions (also called OWL FA-classes and
OWL FA-properties, respectively).
OWL FA has a model theoretic semantics, which is regarded as an
extension of that of RDFS(FA) with interpretations for OWL FA
descriptions and axioms. In the rest of the paper, we assume that
i is an integer such that 1 ![]() i
i ![]() k. The
interpretation function can be extended to give semantics to
OWL FA-properties and OWL
FA-classes. Let
k. The
interpretation function can be extended to give semantics to
OWL FA-properties and OWL
FA-classes. Let
![]() be an abstract property name in stratum i
and
be an abstract property name in stratum i
and ![]() an abstract property in stratum i. Valid OWL FA abstract
properties are defined by the abstract
syntax:
an abstract property in stratum i. Valid OWL FA abstract
properties are defined by the abstract
syntax:
![]() where for some
where for some
![]() ,
,
![]() iff
iff
![]() .
Valid OWL FA datatype properties are
datatype property names.
.
Valid OWL FA datatype properties are
datatype property names.
Now we define the OWL FA-class descriptions. Let
![]() be an atomic class name in stratum i,
be an atomic class name in stratum i, ![]() an
OWL FA-property in stratum i,
an
OWL FA-property in stratum i,
![]() an individual,
an individual,
![]() a datatype property name,
and
a datatype property name,
and ![]() OWL FA-classes in
stratum i.
Valid OWL FA-classes are defined by the abstract syntax:
OWL FA-classes in
stratum i.
Valid OWL FA-classes are defined by the abstract syntax:
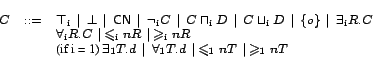
![[*]](crossref.png) ).
).
An OWL FA knowledge base consists of
k. Each
![]() consists of
a TBox , an RBox and an
ABox . Due to the limitation of space, we only present class
and individual axioms here, and leave out the property axioms
in RBoxes.
An OWL FA TBox is a finite
set of class inclusion
axioms of the form
consists of
a TBox , an RBox and an
ABox . Due to the limitation of space, we only present class
and individual axioms here, and leave out the property axioms
in RBoxes.
An OWL FA TBox is a finite
set of class inclusion
axioms of the form
![]() , where
, where ![]() are OWL
FA-classes in stratum i. An interpretation satisfies
are OWL
FA-classes in stratum i. An interpretation satisfies
![]() if
if
![]() .
.
Let a, b
![]() be individuals,
be individuals, ![]() a
class in stratum 1,
a
class in stratum 1, ![]() an abstract property in stratum 1,
an abstract property in stratum 1, ![]() a
literal,
a
literal, ![]() a datatype property,
a datatype property, ![]() classes or
abstract properties in stratum i,
classes or
abstract properties in stratum i, ![]() a class in stratum i + 1 and
a class in stratum i + 1 and
![]() an abstract property in stratum i+1. An OWL FA ABox
an abstract property in stratum i+1. An OWL FA ABox
![]() is a finite set of individual axioms of the following
forms:
is a finite set of individual axioms of the following
forms:
![]() ,
called class
assertions,
,
called class
assertions,
![]() ,
called abstract property
assertions,
,
called abstract property
assertions,
![]() ,
called datatype property
assertions,
,
called datatype property
assertions,
![]() , called individual equality axioms and ,
, called individual equality axioms and ,
![]() , called individual inequality axioms. An
interpretation satisfies
, called individual inequality axioms. An
interpretation satisfies
![]() if
if
![]() ; it satisfies
; it satisfies
![]() if
if
![]() ; it satisfies
; it satisfies
![]() if
if
![]() ; it satisfies
; it satisfies
![]() if
if
![]() ; it satisfies
; it satisfies
![]() if
if
![]() . An OWL FA ABox is
a finite set of axioms of the following forms:
. An OWL FA ABox is
a finite set of axioms of the following forms: ![]() ,
called meta-class
assertions,
,
called meta-class
assertions, ![]() ,
called meta-property
assertions, or
,
called meta-property
assertions, or
![]() , called meta individual equality axioms. An
interpretation satisfies
, called meta individual equality axioms. An
interpretation satisfies ![]() if
if
![]() ; it satisfies
; it satisfies ![]() if
if
![]() ; it satisfies
; it satisfies
![]() if
if
![]() .
.
An
interpretation satisfies a knowledge base if it satisfies all the axioms in .
is
satisfiable (unsatisfiable) iff there exists (does not
exist) such an interpretation that satisfies .
Let ![]() be OWL FA-classes in stratum i,
be OWL FA-classes in stratum i, ![]() is satisfiable
iff there exist an interpretation of s.t.
is satisfiable
iff there exist an interpretation of s.t.
![]() ;
; ![]() subsumes
subsumes ![]() iff for every interpretation of
we have
iff for every interpretation of
we have
![]() .
.
Now we briefly discuss some reasoning tasks of OWL FA. In an OWL FA knowledge base , it is obvious that 1 is a knowledge base, and 2, ..., k are knowledge bases. Note that classes and property names in i are treated as individual names in i+1; therefore, class and property equality axioms in i can act as individual equality axioms in i+1. On the other hand, individual equalities explicitly asserted and implicitly entailed by number restrictions in i+1 can act as class and property equality axioms in i.

As we have a finite set of vocabulary, we have the following
Lemma.
It can be argued that, in many realistic ontologies, would not be much bigger than . This is based on the observation that the number of entailed but not explicit stated equal class (property, individual) pairs would not be huge (as usually it is not extremely helpful to have multiple class names for the same class description). On the other hand, the entailed equalities often come as a surprise for ontology builders.
Note that if a class description is not defined
in ![]() (i.e., if it is not equivalent to any atomic class), it is not represented by any meta-individual in
(i.e., if it is not equivalent to any atomic class), it is not represented by any meta-individual in
![]() . This suggests the connections between
. This suggests the connections between ![]() and
and
![]() are atomic classes and properties in
are atomic classes and properties in ![]() , which
are meta-individuals in
, which
are meta-individuals in ![]() . Accordingly, once we calculate the
explicit knowledge bases, we can decide the
knowledge base satisfiability
problems locally.
. Accordingly, once we calculate the
explicit knowledge bases, we can decide the
knowledge base satisfiability
problems locally.
Theorem 4 indicates we can reduce the OWL FA-knowledge base satisfiability problem to the OWL DL-knowledge base satisfiability problem.
In this paper, we propose the OWL FA ontology language as a decidable metamodeling extension of OWL DL. The syntax of OWL FA is very similar to that of OWL DL; it introduces a stratum number to attach to OWL FA class constructors and axioms. These numbers can be hidden by tools from the users. The semantics of OWL FA is a natural extension of that of OWL DL, dividing the abstract domain into k sub-domains for k strata.
We have shown that it is possible to make use of existing OWL DL reasoners to reason with OWL FA knowledge bases. Most importantly, we believe that reasoning in OWL FA is not much harder than OWL DL. Firstly, as argued in the previous section, the explicit knowledge base usually would not be much bigger than the original knowledge base . Furthermore, we can often assume that the meta knowledge bases 2, ..., k are more stable and much smaller than 1. Indeed, when 2, ..., k are much simpler and smaller than 1, the reasoning time for much smaller than 1, the reasoning time spent on 2, ..., k can be ignored to some extent. This suggest a clear advantage of the FA semantics over the HiLog semantics [1], which requires implementations of new reasoners to provide research services.
In the future, we plan to implement the construction of explicit knowledge bases so that we can use OWL DL reasoners to reason with OWL FA knowledge bases, and to evaluate it with, for example, the WordNet ontology.