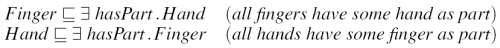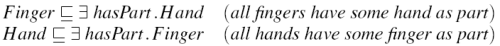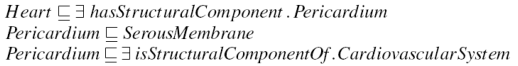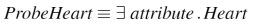Web Ontology Segmentation: Analysis, Classification and Use
1 INTRODUCTION
1.1 The problem of large
ontologies
Ontologies can add tremendous value to web
technologies. As Jim Hendler has pointed out on numerous
occasions ``a little semantics goes a long way'' [11]. The knowledge
captured in ontologies can be used, among other things, to
annotate data, distinguish between homonyms and polysemy,
generalize or specialise concepts, drive intelligent user
interfaces and even infer entirely new (implicit) information.
The ultimate vision for a semantic web is to create an internet that computers can understand and navigate. Making this vision a reality will either require an extremely large ontology that describes every term of interest on the Internet, or, more realistically, numerous domain-specific ontologies, which, when aligned with one another, form a web of semantic inter-ontology relations. Either way, the result is a very large knowledge corpus.
Examples of such enormous ontologies are already starting to appear. For example, the biomedical domain has numerous very large ontologies such as SNOMED-CT [35], GALEN [25], FMA [31] and NCI-Thesaurus [7]. However, these ontologies have grown too large to effectively used and maintained, often requiring large teams of highly trained experts [36].
If a truly massive semantic web is going to be of use to anyone, users and applications will have to find a way to limit their scope. The knowledge web, as a whole, will be too big and mostly irrelevant for any single task.
1.2 Solutions to the scaling
problem
Google solves the problem of scaling web search
by creating partially sorted barrels of keyword indexes.
Searches are distributed over a very large cluster of computers
[5]. A
similarly sophisticated distributed system may be feasible for
use with the ontologies of the semantic web. However,
ontologies, such as those represented in the Web Ontology
Language (OWL) [19], are significantly
more complex data structures than mere web pages. OWL builds
several levels of complexity on top of the XML of conventional
web data [4]
[12]. It is
likely that large and complex ontologies will require a novel
solution.
This paper suggests such a solution: instead of attempting to capture the entire semantic web in a gigantic index, each web application extracts and uses a custom ontology segment specific to its particular needs. Segments are big enough to be useful, but not so big that scaling becomes a problem.
The ontology segmentation techniques shown in this paper exploit the semantic connections between ontology terms and thereby enable web-application developers to quickly (or even automatically) create the custom ontologies they require. This is a first step towards a working application layer on top of a large-scale semantic web.
1.3 Other applications for segmentation
Custom ontology
segments, as described above, show potential for a wide variety
of use cases. For example:
- Query efficiently could be substantially improved by querying segments instead of querying the complete ontology network.
- Segments could be used as examples of and discussion points for specific modeling patterns.
- Segments could be captured at specific time points as backup or provenance data.
- Similar segments from different ontologies in the same domain could be used for comparison and evaluation purposes.
- Segmentation could be used to specify, outline and annotate specific ontology sub-sections.
- Segments from general purpose ontologies could be transformed on-the-fly during the extraction process to produce optimal ontologies for a specific applications.
1.4 GALEN
The research
presented in this paper uses the GALEN ontology of medical
terms and surgical procedures (produced during the 1990s by the
University of Manchester in the OpenGALEN project [29]) as a test platform for
such an ontology segmentation algorithm. Since the complete
GALEN ontology was only available in its own proprietary
format, it was converted into an OWL representation for the
purposes of this research. Only small, incomplete versions of
GALEN in OWL have previously been available.
GALEN serves as an excellent test case because it is both large and complex. It also utilizes much of the expressive power of modern description logics, whereas other large ontologies more closely resemble simple controlled vocabularies. If an effective segmentation algorithm can be demonstrated for something as complex as GALEN, we can therefore expect it to also work well for the complex large ontologies of the future.
1.5 Scope
The algorithm represented in this paper is
optimized to work with knowledge bases similar to the GALEN
ontology. That is, a large ontology with over 1000 classes and
dense connectivity, with at least, on average, one restriction
asserted per concept.
Another pre-requisite for our segmentation methodology is that the ontology be normalised [26]. Primitive classes in a normalised ontology have no more than one primitive superclass: multiple parents are modeled implicitly and left to be explicitly inferred later. Normalisation greatly simplifies ontology maintenance.
GALEN in OWL uses the SHIF subset (without negation or disjunction) of the full SHOIN(D) expressivity of OWL-DL, so the segmentation is currently constrained to that. The methodology presented here is not meant to offer a complete solution with rigorous logical proofs. Instead, we present empirical evidence as to the effectiveness of our approach.
Most ontologies' properties are structured as flat lists. GALEN however employs a rich property hierarchy with over 500 distinct properties. This is especially useful for producing extracts constrained to specific user and/or application requirements. Ontologies with simple property structures, such as, for example, the Gene Ontology [34], will not be able to take advantage of this aspect of the segmentation algorithm presented herein.
1.6 Aim: useful classification and small size
Description
logic reasoners such as FaCT++ [38], RACER [10], or Pellet [23] can be used to infer
new information that is implicit in an ontology [16]. This process is very
important, especially for an ontology like GALEN, which was
built with normalisation principles in mind. It is therefore
critical that GALEN in OWL can be classified.
However, none of the above mentioned description logic reasoners based on the tableaux algorithm are currently able to classify the complete GALEN ontology. GALEN is too large and complex for these reasoning systems. A primary aim of this research was therefore to produce classifiable segments. The ideal segment is as small and focused as possible, while still containing enough information to enable the reasoner to infer relevant new subsumption relationships.
2 LINKS IN DESCRIPTION
LOGIC
2.1 Superclasses as links
OWL ontologies usually contain
large hierarchies of concepts. They also feature the ability to
add restrictions to such concepts. The most common types
of restrictions restrict the individuals that a
certain class describes. These restrictions are
quantified by, for example, the existential
or universal quantifiers. Quantified restrictions also include a property
and filler concept to specify how the members of a class
are restricted.
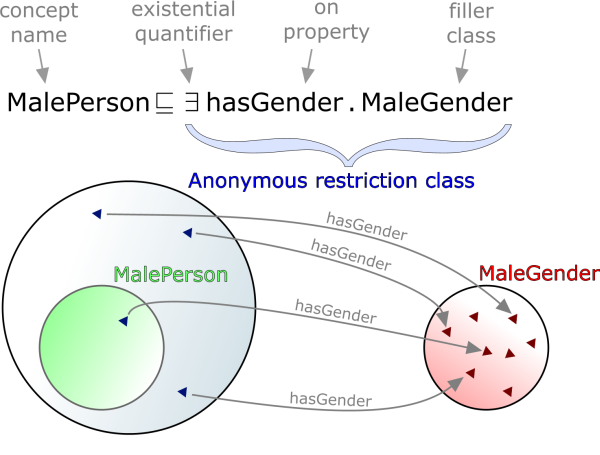
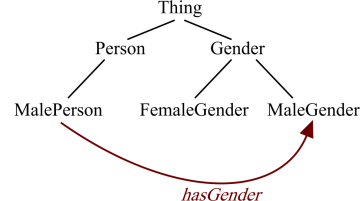
Restrictions, from one point-of-view, are anonymous classes and can be added as superclasses of another (named) class. For example: the class MalePerson might have the restriction in Figure 1 asserted as its superclass. This means that all individuals that the MalePerson class defines must have one or more relations using the hasGender property to individuals in the class MaleGender. Figure 1 illustrates this relationship.
However, seen from another point-of-view, restrictions represent cross-links between different classes as shown in Figure 2, so that an ontology can be seen as a large hierarchy of classes linked by restrictions.
In reality, of course, the anonymous qualified restriction superclasses actually restrict individuals' relations to other individuals, but it is useful to think of them simply as links. This paper will, from here on, assume this model of ontological topology.
2.2 Reciprocal
links
Besides normal forward links, as described above,
backward links, or usages, also known as reciprocal
links, are also important in understanding the structure of
an ontology.
Even though ``isPartOf'' and ``hasPart''are inverses of each other, the reciprocal statements in Figure 3 are not equivalent; in fact neither implies the other.
GALEN is unusual in that it commonly represents anatomy using reciprocal pairs of restrictions. This representation is inherently cyclical and connects every piece of anatomy with every related piece in both directions. Tableaux classifiers intrinsically scale exponentially when faced with such constructs. None of the current tableaux-based reasoners listed in Section 1.6 can classify even a small extract of the GALEN ontology containing both types of reciprocal links present in the original. (Note: the original classifier used in GALEN used different principles and did not suffer from this particular limitation [13].)
The algorithm presented herein therefore takes the approach of taking all reciprocals into account, but producing actual segments with only one-way links, using, for example, only ``isPartOf'' relations. Some of the new relations may be virtual: i.e. have only been found by first adding the reciprocals.
It is important to note that these reciprocal links differ from symmetric links. That statement in Figure 4 is a symmetric link, which has a very different meaning to the example of a reciprocal link given above. Symmetric links do not adversely affect classification.
3 BASIC SEGMENTATION ALGORITHM
The basic segmentation
algorithm starts with one or more classes of the user's choice
and creates an extract based around those and related concepts.
These related classes are identified by following the ontology
link structure.
3.1 Upwards traversal of the
hierarchy
Assuming, for example, that a segment of the
Heart class is to be produced. The obvious first class
to include is the Heart, the Heart's superclass
(InternalOrgan), then that class' superclass and so on, all the
way up the hierarchy, until the top
concept is reached. Since this hierarchy is often quite deep
(13 superclasses in this case) one might consider collapsing
the tree by merging several superclasses. However, this
destroys some of the semantic accuracy of the ontology. It may
be sensible when constructing an ontology view or
perspective, but is not useful for any extract that is
to be used in an application (such as a classifier), since each
superclass might contain critical information.
3.2 Downwards traversal of the
hierarchy
The algorithm also goes down the class
hierarchy from the Heart, including its subclasses (in
this case: UniventricularHeart). This is especially relevant
when segmenting an ontology that has already been classified
where newly inferred subclasses of a particular class are
likely to be of interest.
The property hierarchy is however never traversed downwards. Properties are not of interest unless they are used in the class hierarchy. So, if they are used, they, their superproperties and no other properties, are included.
3.3 Sibling classes in the
hierarchy
Sibling classes are not included in the
extract. The Heart class' siblings include concepts like
the Lung, Liver and Kidney. It is
reasonable to assume that these are not relevant enough to be
included by default. The user can always explicitly select them
for inclusion, if they are of interest.
3.4 Upwards & Downwards and Upwards from links
Having
selected the classes up & down the hierarchy from the
target class, their restrictions, intersection, union and
equivalent classes now need to be considered: intersection and
union classes can be broken apart into other types of classes
and processed accordingly. Equivalent classes (defined classes
which have another class or restriction as both their subclass
and their superclass) can be included like any other superclass
or restriction, respectively. Restrictions generally have both
a type (property) and a filler (class), both of
which need to be included in the segment.
Additionally, the superproperties and superclasses of these newly included properties and classes also need to be recursively included, otherwise these concepts would just float in OWL hyperspace. That is, without being attached to the hierarchy, concepts are assumed to simply be subsumed by the top concept, leading to a very messy, confusing and often semantically incorrect view of the unclassified ontology.
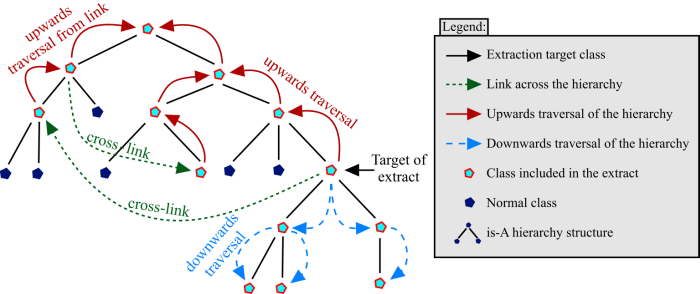
Figure 5 gives an illustration of this segmentation algorithm. Starting at the target of the extract, the algorithm traverses the hierarchy upwards all the way to the root class. It also traverses it downwards all the way to the leaf classes. Additionally, any links across the hierarchy from any of the previously traversed classes are followed. The hierarchy is traversed upwards (but not downwards) from any of these classes that the cross-links point to. Links pointing at other classes from these newly traversed classes are also included. This continues until there are no more links left to follow.
3.5 But not Downwards from Upwards links
Finally, one might
also consider including the subclasses of those classes
included via links. However, doing so would result in including
the entire ontology. This is something one definitely wants to
avoid when creating an extract.
4 CONSTRAINING SEGMENT
SIZE
The segmentation algorithm outlined above produces
an extract of all concepts related to the target concept.
However, with densely interconnected ontologies, such as for example GALEN,
this new ontology is usually only up to one fifth the size of
the original. A means of further constraining segments is
needed.
4.1 Property filtering
If the aim is to produce a segment for
use by a human, or specialized application, then filtering on
certain properties is a useful approach.
For example, if a user is not interested in the diseases modeled in GALEN, he or she can specify to exclude all locative properties. These are properties that specifically link diseases to the locations in the body where they might occur: e.g. ``IschaemicCoronaryHeartDisease hasLocation Heart''.
The upper-level meta-properties which it may be logical to include and/or exclude will be different for each ontology to be segmented. These meta-properties are, in this case, actual properties, since GALEN groups related properties together under super-properties. The following meta-properties and their inverses were selected for course grain property filtering:
- modifierAttribute: properties which can be used to modify a given class such as ``colour'' or ``status''. These are sometimes also known as ``value partitions'' [6]. They are almost always safe to include in an extract, since the class values they link to do not themselves link onwards to other classes and therefore will not significantly increase a segment's size.
-
constructiveAttribute: the super-property of all the
following properties.
- locativeAttribute: properties that link diseases to anatomical locations that they are in some way related to.
- structuralAttribute: properties linking anatomical body structures together by physical composition.
- partitiveAttribute: properties that link classes based on processes, divisions and other partitive relations
- functionalAttribute: properties that link classes by action or function.
Note: The various properties could be broken down much more elaborately. However, the point is that organizing properties under any sensible upper-level property structure will enable some degree of useful property filtering. A more detailed analysis of the GALEN property hierarchy may be found in [30].
4.1.1 Removing trivially equivalent definitions
Properties are
filtered by removing all restriction in which they occur.
However, upon removing such restrictions from defined class, it
frequently occurs that a definition becomes indistinguishable
and therefore equivalent to another similar definition. The
resultant long chains of equivalent classes, while not wrong,
are difficult to view in ontology editors (such as Protégé OWL
[14]).
Trivially equivalent definitions are therefore transformed into
primitive classes by the segmentation algorithm. These still
occupy the correct place in the hierarchy and are easy for
editors to display.
As shown in the progression in Figure 6, if the filtering process removes the restriction on a class and this results in a trivial equivalence, then the definition is converted into a primitive class.
4.2 Depth limiting using boundary classes
Depth limiting is a
useful approach for accurately adjusting the size of a segment
so that it can, for example, be classified successfully by
automated reasoners.
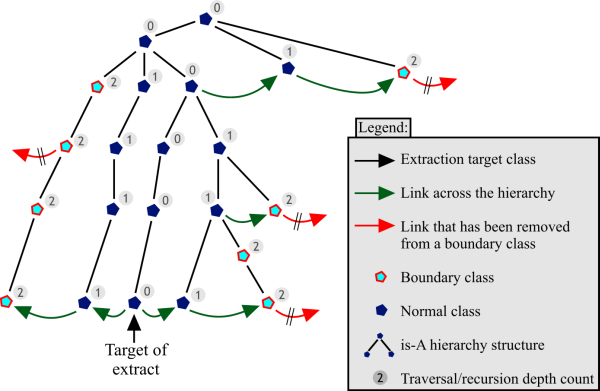
A chain of links is followed to create a list of classes to include in an extract. In doing so, each classes' restrictions' filler classes should be included to produce a semantically correct extract (see Sections 2.1 and 3.4). However, if, upon reaching a certain recursion depth, calculated from the extract's target concept, all the links on a class are removed, this class becomes a boundary class.
For example, one might remove the axiom in Figure 7 stating that the Pericardium (the membrane that surrounds the heart) is a component of the CardiovasuclarSystem (line three of the Figure), since one may not be interested in including the CardiovascularSystem and everything related to it in a segment of the Heart. This creates a boundary class that is still defined in the hierarchy (under SerousMembrane) and therefore still makes sense within the ontology, but has an incomplete definition.
The named superclasses of a boundary class (line two of Figure 7) must be included in the extract in order to place classes in their proper position in the hierarchy. These classes would otherwise all be subsumed under the top concept. These superclasses are however also boundary classes, unless they are linked to by way of shorter recursion path along another concept, as shown in Figure 8.
The main hierarchy of ``is-A'' superclass relationships between classes should not be counted when calculating the traversal depth, since they need to be included in any case and do not substantially increase the complexity of the segment. Subclass relations can be ignored completely, since they are not included in the extract in the first place (see Section 3.5). Figure 8 illustrates the entire boundary extraction procedure.
This methodology effectively limits the size of the ontology, since the presence of a boundary class will cause a link traversal algorithm to terminate. Otherwise, in the case of a densely interlinked ontology such as GALEN, practically the entire ontology could be ``linked-in''.
Noy and Musen's ontology extraction research [21], also uses the boundary class term, but defines it as any class which is in the range of any property that is used in each restriction on each of the classes which are targeted by the extract. The resulting list of boundary classes is to function as a reminder to the user of other classes they might want to include in the view they are constructing. This approach relies on property ranges being specified in the ontology, which is often not the case and on a graphical user interface to ``prompt'' [20] the user. The approach presented here takes a more automated approach, aiming to produce a heuristic algorithm that creates a useful segment without much user intervention.
5 EVALUATION
The utility
of various segmentation strategies with regards to applications
can not be evaluated at this time, because suitable
applications that take advantage of segmented ontologies do not
yet exist. However, the performance of this methodology can be
evaluated by various statistical measures.
(Tests were carried out on a 2.8 Ghz Pentium 4 with 2.5 GB of RAM running Racer 1.8.0 on Windows XP service pack 2.)
5.1 Segmentation speed
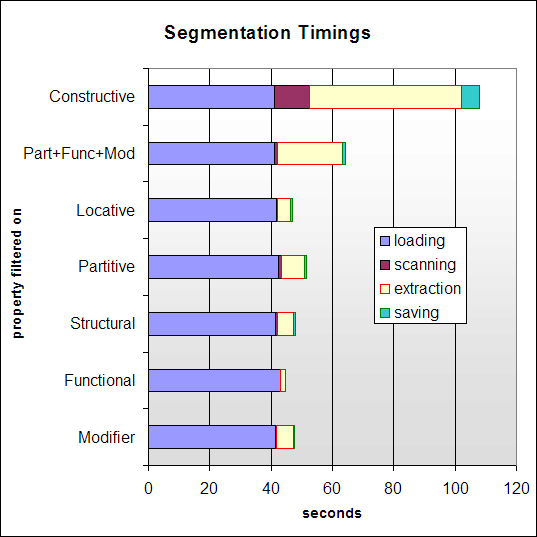
Figure 9 gives a breakdown of
how long various aspects of the segmentation process take. The
first step is loading the target ontology. The next involves an
initial pass over the ontology, scanning for and marking the
classes to include in the eventual segment extraction process.
Extraction constructs a new, self-contained ontology segment,
which is then saved to disk.
As can be seen from the figure, the complete segmentation process takes an average of one minute to complete. However, most time is spent loading the ontology. Once the target ontology is in memory, the segmentation itself takes only around six seconds to complete. It can be observe that segments from large ontologies can be created with good computational efficiency, though this is, of course, dependent on the specific implementation of the extraction algorithm.
Performance is currently not fast enough for real-time user queries. However, the results show good potential for future optimisations, especially if loading times can be reduced by streaming segmentation techniques and/or caching. Furthermore, segmentation is not meant to replace querying. Instead, it enables efficient querying of otherwise intractable ontologies.
5.2 Basic segmentation
The
basic segmentation algorithm targeted around the GALEN
``Heart'' concept produced the results shown in Table 1. As can be seen from the table, the segment
is roughly a quarter the size of the original ontology, with
the number of properties being reduced the least and the number
of primitive classes being reduced the most. A similar pattern
can be observed when segmenting using different target classes.
This reduction in size is not enough to enable classification given current memory and reasoner applications. All current tableaux algorithm-based description logic reasoner systems stack-overflow when attempting to classify the basic extract of GALEN. The filtering and boundary extraction algorithms do however create classifiable ontology segments (see Section 5.3.2).
5.3 Property filtering segmentation
results
A segment was produced by including only
properties from each of the main property categories identified
in Section 4.1. Segments
using combinations of property categories were also produced.
It was found that the combination of Partitive,
Functional and Modifier properties produced the
largest ontology that could still be classified successfully.
Statistics for this combination segment are therefore also
included in the tables below.
Table 2 gives an overview of the size of various property filtered segments. As can be seen from the results, segments could be reduced in size by an average factor of 20 over the original ontology and by a factor of five over the basic extraction methodology.
5.3.1 Probe classes
The test query (probe class) in Figure 10 was introduced into every segmented ontology to test its classification performance. An approximate measure of the degree of knowledge present in a segment may be obtained by counting the number of new classes inferred as subclasses of the probe. The probe effectively answers the query ``everything related to the Heart'' by using the ``attribute'' property, which is the top-level property in GALEN.
5.3.2 Classification tests
Table 3 shows several classification
statistics:
Note: the ``new inferences'' column only lists new inferences under the probe class. Many other new subclass relationships are inferred in each segment, but these are not necessarily relevant to the extract's target concept and were therefore not counted as part of this evaluation.
5.3.3 Discussion
- The segment using all Constructive properties (combination of Structural, Locative, Functional and Partitive properties) was too large to classify.
- The Functional and Partitive segments produced the most new inferences relative to their size. This indicates that a majority of the knowledge in GALEN is covered by these two structures.
- As expected, the Modifier properties do not add very much complexity to a segment and are therefore almost always safe to include in any segment.
- Structural properties do not play a major role in the ontology, since they do not add much information.
- Locative properties are of small, but not insignificant consequence to the classification. This indicates that complexity of the anatomical model in GALEN is far greater than the complexity of disease model.
5.4 Boundary class segmentation
results
5.4.1 Boundary size
results
As one might expect, the boundary extraction
algorithm produces progressively smaller segments, in
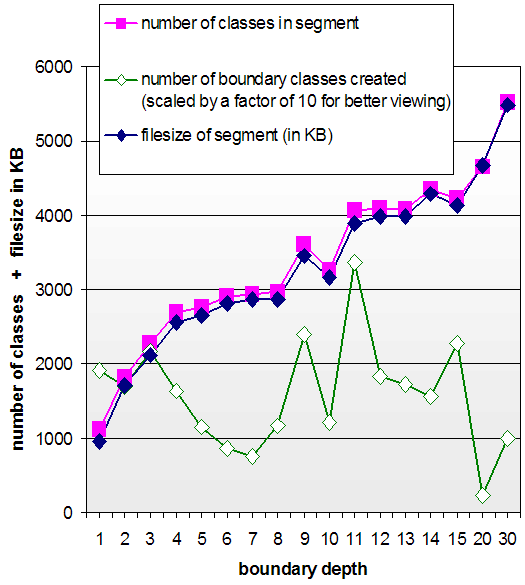
proportion with the boundary cut-off. However, there seems to
be no correlation between the number of boundary classes
created at each cut-off level and the size of the resultant
ontology. Figure 11
illustrates the differences in boundary sizes.
This result indicates that the link structure of the GALEN ontology is very interwoven and unpredictable. There seem to be no tight group of boundary classes that limit a particular extract and therefore also no way to cleanly divide an ontology into modules. That is, the complex ontological relationships cannot be cleanly divided into fixed categories. We should therefore expect traditional partitioning methodologies, such as those discussed in Section 6, to be of limited use in this domain.
5.4.2 Boundary classification
results
Table 4 shows the results of the boundary classification testing. Only boundary depth ``one'' could be successfully classified.
Boundary extraction by itself provides a very good means of controlling the size of an extract, but does not seem to provide much optimization for classification. A combination of boundary extraction and filtering segmentation allows one to control both the classifiability and size of a segment. This combination represents the optimal segmentation strategy.
6 RELATED WORK
6.1 Overview
The idea of
extracting a subset of a larger ontology is referred to by many
different names by different authors. Research regarding views,
segments, extracts, islands, modules, packages and partitions
may be broken down into three main categories:
- Query-based methods
- Network partitioning
- Extraction by traversal
The research presented in this paper falls into category three.
6.2 Query-based
methods
Many researchers, taking inspiration from the
databases field, define ontological queries in an SQL-like
syntax. These queries can return sub-ontology segments as their
answer-sets.
6.2.1 SparQL
The SparQL query
language [32]
defines a simple query mechanism for RDF. Multiple queries are
required in order to extract complex knowledge as, for example,
a class and its transitive closure (all classes related
to it). SparQL might be a good low-level tool for implementing
ontology segmentation, but is not a solution in and of itself.
6.2.2 KAON views
Volz and
colleagues define an ontology view mechanism based upon the RQL
query language [39].
They highlight RQL [1] as the only RDF query
language that takes the semantics of RDF Schema into account.
Their view system has the ability to place each concept in its
corresponding place in the complete RDF hierarchy. This
practice, similar to the algorithm presented in Section
3, gives a more complete picture of
the structure of a query answer than merely returning the
relevant concepts in isolation. They do not however provide a
means of materializing a view, i.e. views are transient:
they are discarded as soon as they have served their purpose.
6.2.3 RVL
Magkanaraki and
colleagues present a similar approach to Volz's, except their
system also allows queries to reorganize the RDFS hierarchy
when creating a view [18]. This allows
views to be customized on-the-fly for specific applications'
requirements. They however also side-step the ontology updating
problem by only creating virtual views. Their views are
merely a collection of pointers to the actual concepts, and are
discarded after they have served their purpose.
6.2.4 Discussion
Query-based
methods provide a view mechanism similar to SQL. This makes
them intuitively familiar to computer scientists with a
background in databases. The shortcomings of these approaches
are that they provide only very low-level access to the
semantics of the ontology being queried and do not yet address
the issue of updating the original ontology when an extract is
changed. Query-based views are good for getting very small,
controlled, single-use extracts, which are tightly focused
around a few concepts of interest.
By contrast, the methods presented herein create self-standing, persistent, multi-use ontology segments. That is, the segments have a life of their own: they can be transformed, updated, shared, annotated, plugged into applications and otherwise manipulated in myriad of ways.
6.3 Network
partitioning
The basic idea of partitioning comes from
Herbert Simon. He asserts that any system has the property of
near-complete decomposability [33]. That is, we can always
find clusters of objects that are more related to each other
than to the other objects around them. How complete a
decomposition is possible depends on the nature of the system
in question.
Researchers in networking use algorithms to organize the nodes on a network into inter-related islands [2]. Some ontology researchers propose applying a similar methodology to segmenting ontologies.
An ontology can, from this point of view, be viewed as a network of nodes connected by links. The class hierarchy can be interpreted as a directed acyclic graph (DAG) and any relations between classes can be represented as links between the nodes (a simplified model of the paradigm presented in Section 2.1).
6.3.1 Structure-based
partitioning
Stuckenschmidt and Klein present a method
of partitioning the classes hierarchy into modules [36]. They exploit
the structure of the hierarchy and constraints on properties'
domains and ranges (for example: the ``hasGender'' property
might have a domain of ``Animal'' and a range of ``Male or
Female'') to iteratively break the ontology up into dynamically
sized modules. This method does not take OWL restrictions,
which can act as additional links between concepts, into
account. Instead it relies on the globally asserted domain
& range constraints. However, domains and ranges are
optional and may not therefore be asserted in a given ontology.
Structure-based partitioning is primarily meant for breaking an ontology into broad packages or modules so that it can be more easily maintained, published and/or validated. However, this process destroys the original ontology, leaving it decomposed into whatever modules the partitioning algorithm deemed appropriate. Moreover, ontologies, particularly those modeled in OWL, tend to be more semantically rich than a simple network abstraction will capture.
6.3.2 Automated Partitioning using
E-connections
Grau and colleagues [8] present a method for
modularizing OWL ontologies similar to Stuckenschmidt and
Klein's approach [36]. However, they
address the issue of the original ontology being destroyed by
using  -connections [15] to keep the individual
modules somewhat interconnected. The modularized ontology
fragments produced by their algorithm are formally proven to
contain the minimal set of atomic axioms necessary in order to
maintain crucial entailments.
-connections [15] to keep the individual
modules somewhat interconnected. The modularized ontology
fragments produced by their algorithm are formally proven to
contain the minimal set of atomic axioms necessary in order to
maintain crucial entailments.
While Grau's approach is formally sound, it does not seem to scale up to complex, large ontologies. In particular, tests using a 3000-class fragment of GALEN failed to produce a useful segmentation. The methodology does not seem to be able to modularize ontologies that make use of an upper-ontology [9]. Since many large ontologies rely on such an upper ontologies to maintain a high-level organizational structure [24], Grau's approach is only of limited real-world use.
6.3.3 SNARK and
Vampire
MacCartney et al. use the same
partitioning idea to solve a different problem: they present a
first-order logic theorem prover (SNARK) [17], which decomposes
the knowledge base into self-contained mini-prover partitions,
which then communicate with each other using message passing
techniques. The researchers thereby successfully improve the
efficiency of their reasoning algorithm when answering queries
over large knowledge bases.
Tsarkov and Horrocks [37] use a similar approach for optimizing the classification performance of the Vampire first-order logic theorem prover [28] when classifying description logic ontologies.
6.4 Extraction by
traversal
Ontology extraction by traversal, similar to
the network partitioning approach, also sees the ontology as a
networking or graph. However, instead of decomposing the entire
graph into modules, this methodology starts at a particular
node (concept) and follows its links, thereby building up a
list of nodes (concepts) to extract. A key difference is that
this leaves the structure of the original ontology intact: it
creates an extract, not a decomposition.
6.4.1 PROMPT
Noy and Musen present an
extension to the PROMPT suite [20] of ontology maintenance
tools, which are themselves plug-ins to the Protégé ontology
editor [22]. Their
extraction methodology [21] focuses on traversal
directives, which define how the ontology links should be
traversed. Collections of directives completely and
unambiguously define an ontology view and can themselves be
stored as an ontology. They also introduce the concept of
boundary classes around the edges of an extract.
However, their view of boundary classes differs from the
perspective given in this paper (see Section 4.2).
Noy's research establishes the mechanics of ontology view extraction, but does not address how her system might be used to construct relevant, useful and computationally tractable segments.
6.4.2 MOVE
Bhatt, Wouters and
company have a different focus: They present the Materialized
Ontology View Extractor (MOVE) system for distributed
sub-ontology extraction [3]. It is a generic system
that can theoretically be adapted to work with any ontology
format. The system extracts a sub-ontology based on a user's
labelling of which ontology terms to include and which to
exclude. It also has the ability to optimise an extract based
upon a set of user selectable optimisation schemes. These
schemes can produce either the smallest possible extract, a
medium size one, or include as much detail as possible. These
extracts can be further restricted by enforcing a set of
additional constraints. Their system can, for example, enforce
the semantic completeness and well-formedness of an extract
[40].
However, the primary focus of Bhatt and Wouters' architecture is parallel processing. While, their extract system performs very poorly when run on a single machine (17 minutes to produce an extract from a 5000-concept ontology), it achieves optimum performance using around five separate processors.
We argue that speed is not a critical factor in the extraction process. Performance is too poor to facilitate an instant, on-demand extraction web-service, but not poor enough that it becomes a serious problem. For example, extraction tests on the GALEN ontology by these authors took in the order of two to five minutes to complete.
6.4.3 Discussion
Both MOVE and PROMPT produce a materialized view, i.e. a self-standing ontology that has no direct connection with its origin. Both also have the notion of the transitive closure of a concept (Wouters et al. call this semantic completeness [40]). However, neither methodology addresses the important issue of how to update the main ontology if the view is modified, how to transform the ontology on-the-fly while extracting, nor do they discuss the ability to classify an extract using description-logic reasoning systems. Finally, neither systems make use of meta-information about an ontology's semantics in determining the best extract. The user must make a great deal of manual selections and choices for each new extract he or she wishes to produce.
By contrast, the segmentation algorithms presented herein automates the extraction process as much as possible by taking advantage of meta-information. Additionally, these methods have the ability to transform the extracted ontology segments (see Section 4.1.1) and are optimized for enabling classification.
The key difference between the approach present here and the other approaches is that we do not aim to create views of one type or another. Instead, we aim to produce independently useful and usable ontologies.
7 FUTURE WORK
The GALEN
ontology was chosen as a proof-of-concept test-case for the
segmentation techniques presented herein. The next step is to
generalise the algorithm to work well with other well-known
large ontologies and ultimately to work well with any large
ontology within the algorithm's scope (see Section 1.5).
Such a generic algorithm will then be integrated with ontology alignment methodologies, thereby making it possible to produce extracts that cut across ontology borders. Such a segmentation algorithm, offered as a web service, will make it possible to create ontology segments from a web of ontologies: an otherwise unmanageable semantic web will become tractable for computers and comprehendible for humans.
Additionally, other applications and evaluations of the segmentation methodology (as outlined in Section 1.3) will be explored in the future.
8 CONCLUSION
Ontologies
with over ten-thousand classes suffer severely from scaling
problem. Segmentation by traversal is a way of overcoming these
difficulties. Developers can use ontology segmentation
techniques to quickly and easily create the relevant,
self-standing custom ontologies they require, instead of having
to rely on the initial authors' decomposition. Ontology
segments can be specialized further by only including links of
specific types in the extract (property filtering), limiting
the depth of the link traversal algorithm (boundary
extraction), or a combination of both.
The methods presented take advantage of many ontology maintenance principles: normalisation [26], upper-ontologies [24] and rich property hierarchies [25] are all taken into account in order to produce more relevant segments. Other approaches to segmentation do not take advantage of many of the semantics captured within an OWL ontology and are therefore only of limited use.
Evaluation has shown that segmenting ontologies can decrease their size considerably and significantly improve their performance. The size of the GALEN ontology was reduced by a factor of 20. Moreover, segments of this ontology, which was previously impossible to classify, were classified within seconds. Additionally, useful insights into the ontology meta-structure were gained from the analysis of various segments.
The complete GALEN in OWL along with a web application that can generate custom GALEN segments is available online1.
REFERENCES
- 1
- S. Alexaki, V. Christophides, G. Karvounarakis, D.
Plexousakis, K. Tolle, B. Amann, I. Fundulaki, M. Scholl, and
A.-M. Vercoustre.
Managing RDF Metadata for Community Webs.
In ER '00: Proceedings of the Workshops on Conceptual Modeling Approaches for E-Business and The World Wide Web and Conceptual Modeling, pages 140-151, 2000. - 2
- V. Batagelj.
Analysis of large network islands.
Dagstuhl Semina 03361, University of Ljubljana, Slovenia, August 2003.
Algorithmic Aspects of Large and Complex Networks. - 3
- M. Bhatt, C. Wouters, A. Flahive, W. Rahayu, and D.
Taniar.
Semantic completeness in sub-ontology extraction using distributed methods.
In A. Laganŕ, M. L. Gavrilova, and V. Kumar, editors, Computational Science and Its Applications (ICCSA), volume 3045, pages 508 - 517. Springer-Verlag GmbH, May 2004. - 4
- T. Bray.
What is RDF?,
http://www.xml.com/pub/a/2001/01/24/rdf.html, January 2001. - 5
- S. Brin and L. Page.
The anatomy of a large-scale hypertextual Web search engine.
Computer Networks and ISDN Systems, 30(1-7):107-117, 1998. - 6
- N. Drummond, M. Horridge, H. Wang, J. Rogers, H.
Knublauch, R. Stevens, C. Wroe, and A. Rector.
Designing User Interfaces to Minimise Common Errors in Ontology Development: the CO-ODE and HyOntUse Projects.
In S. J. Cox, editor, Proceedings of the UK e-Science All Hands Meeting, September 2004. - 7
- J. Golbeck, G. Fragoso, F. Hartel, J. Hendler, J.
Oberthaler, and B. Parsia.
National Cancer Institute's Thésaurus and Ontology.
Journal of Web Semantics, 2003. - 8
- B. C. Grau, B. Parsia, E. Sirin, and A. Kalyanpur.
Automatic Partitioning of OWL Ontologies Using E-Connections.
In International Workshop on Description Logics, 2005. - 9
- B. C. Grau, B. Parsia, E. Sirin, and A. Kalyanpur.
Modularizing OWL Ontologies.
In K-CAP 2005 Workshop on Ontology Management, October 2005. - 10
- V. Haarslev and R. Möller.
RACER System Description.
In R. Goré, A. Leitsch, and T. Nipkow, editors, Automated Reasoning: First International Joint Conference, volume 2083 / 2001, page 701. Springer-Verlag Heidelberg, June 2001. - 11
- J. Hendler.
On beyond ontology.
Keynote talk, International Semantic Web Conference, 2003. - 12
- I. Horrocks, P. F. Patel-Schneider, and F. van
Harmelen.
From SHIQ and RDF to OWL: The making of a web ontology language.
In Journal of Web Semantics, volume 1, pages 7-26, 2003. - 13
- I. Horrocks, A. L. Rector, and C. A. Goble.
A Description Logic Based Schema for the Classification of Medical Data.
In KRDB, 1996. - 14
- H. Knublauch, R. W. Fergerson, N. Noy, and M. A.
Musen.
The Protégé OWL Plugin: An Open Development Environment for Semantic Web Applications.
In Third International Semantic Web Conference (ISWC 2004), 2004. - 15
- O. Kutz, C. Lutz, F. Wolter, and M. Zakharyaschev.
E-connections of abstract description systems.
In Artificial Intelligence, volume 156, pages 1-73, 2004. - 16
- C. Lutz, U. Sattler, and L. Tendera.
The complexity of finite model reasoning in description logics.
In F. Baader, editor, Automated Deduction, pages 60 - 74. Springer-Verlag Heidelberg, 2003. - 17
- B. MacCartney, S. McIlraith, E. Amir, and T. E.
Uribe.
Practical Partition-Based Theorem Proving for Large Knowledge Bases.
In Proceedings of the Nineteenth International Conference on Artificial Intelligence (IJCAI-03), pages 89-96, 2003. - 18
- A. Magkanaraki, V. Tannen, V. Christophides, and D.
Plexousakis.
Viewing the Semantic Web through RVL Lenses.
Journal of Web Semantics, 1(4):29, October 2004. - 19
- D. L. McGuinness and F. van Harmelen.
OWL Web Ontology Language Overview, February 2004.
W3C Recommendation. - 20
- N. Noy and M. A. Musen.
The PROMPT Suite: Interactive Tools For Ontology Merging And Mapping.
International Journal of Human-Computer Studies, 59(6):983-1024, 2003. - 21
- N. Noy and M. A. Musen.
Specifying ontology views by traversal.
In S. A. McIlraith, D. Plexousakis, and F. van Harmelen, editors, International Semantic Web Conference, volume 3298 of Lecture Notes in Computer Science, pages 713-725. Springer, November 2004. - 22
- N. F. Noy, R. W. Fergerson, and M. A. Musen.
The Knowledge Model of Protégé-2000: Combining Interoperability and Flexibility.
In EKAW '00: Proceedings of the 12th European Workshop on Knowledge Acquisition, Modeling and Management, pages 17-32. Springer-Verlag, 2000. - 23
- B. Parsia and E. Sirin.
Pellet: An OWL DL reasoner.
ISWC 2004, 2004.
ISWC. - 24
- A. Pease, I. Niles, and J. Li.
The suggested upper merged ontology: A large ontology for the semantic web and its applications.
In Working Notes of the AAAI-2002 Workshop on Ontologies and the Semantic Web, July 28-August 1 2002. - 25
- A. Rector and J. Rogers.
Ontological Issues in using a Description Logic to Represent Medical Concepts: Experience from GALEN.
In IMIA WG6 Workshop, 1999. - 26
- A. L. Rector.
Normalisation of ontology implementations: Towards modularity, re-use, and maintainability.
In Proceedings Workshop on Ontologies for Multiagent Systems (OMAS) in conjunction with European Knowledge Acquisition Workshop, 2002. - 27
- A. L. Rector, S. Bechhofer, C. Goble, I. Horrocks, W. A.
Nowlan, and W. D. Solomon.
The GRAIL concept modelling language for medical terminology.
Artificial Intelligence in Medicine, 9(2):139-171, February 1997. - 28
- A. Riazanov and A. Voronkov.
Vampire 1.1 (system description).
IJCAR, (LNAI 2083):376-380, 2001. - 29
- J. Rogers.
OpenGALEN: Making the impossible very difficult,
http://www.opengalen.org/, August 2005. - 30
- J. Rogers and A. Rector.
GALEN's model of parts and wholes: Experience and comparisons.
Proceedings of AMIA Symposium, pages 714-8, 2000 - 31
- C. Rosse and José L. V. Mejino.
A reference ontology for biomedical informatics: the Foundational Model of Anatomy.
Journal of Biomedical Informatics, 36(6):478-500, November 2003. - 32
- A. Seaborne and E. Prud'hommeaux.
SparQL Query Language for RDF,
http://www.w3.org/TR/rdf-sparql-query/, February 2005. - 33
- H. A. Simon.
The Sciences of the Artificial, chapter 7, pages 209-217.
MIT Press, 1969. - 34
- B. Smith, J. Williams, and S. Schulze-Kremer.
The Ontology of the Gene Ontology.
In Proceedings of AMIA Symposium, 2003. - 35
- M. Q. Stearns, C. Price, K. A. Spackman, and A. Y. Wang.
SNOMED clinical terms: overview of the development process and project status.
In Proceedings of AMIA Symposium, pages 662--6, 2001. - 36
- H. Stuckenschmidt and M. Klein.
Structure-Based Partitioning of Large Class Hierarchies.
In Proceedings of the 3rd International Semantic Web Conference, 2004. - 37
- D. Tsarkov and I. Horrocks.
Dl reasoner vs. first-order prover.
In Description Logic Workshop (DL 2003), volume 81 of CEUR, pages 152-159, 2003. - 38
- D. Tsarkov and I. Horrocks.
Reasoner prototype: Implementing new reasoner with datatypes support.
WonderWeb Project Deliverable, 2003. - 39
- R. Volz, D. Oberle, and R. Studer.
Views for light-weight web ontologies.
In Proceedings of the ACM Symposium on Applied Computing (SAC), 2003. - 40
- C. Wouters, T. Dillon, W. Rahayu, E. Chang, and R.
Meersman.
Ontologies on the MOVE.
In Y. Lee, J. Li, and K.-Y. Whang, editors, Database Systems for Advanced Applications (DASFAA): 9th International Conference, volume 2973, pages 812 - 823. Springer-Verlag GmbH, March 2003.