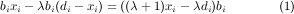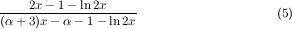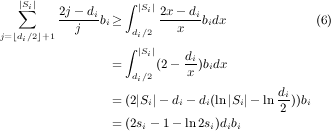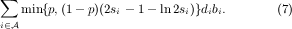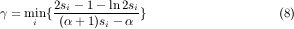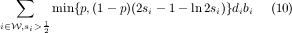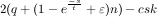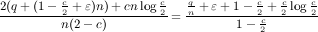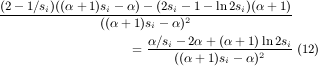1 Introduction
1. Online advertising is one of the most profitable business models for Internet services to date, accounting for annual revenues approaching $17 billion dollars according to the Internet Advertising Bureau [21]. According to the same report, 22% of this revenue comes from banner advertising, or graphic-based advertisements which appear embedded in content pages on a host website. Current models of banner advertising require advertisers to negotiate rates directly with the sales representatives of the host on a monthly basis. These negotiations involve several parameters. First, the advertiser specifies a subset of content pages which are relevant to his or her ad. Next, the advertiser requests a desired number of impressions, or advertising opportunities, on pages from among his or her specified subset, and a per-impression price. Finally, if the negotiation is successful and the contract is accepted, the advertisement is shown on some subset of the specified content pages. By accepting a contract the supplier is committed to the supply. If the supply is not met, the bidder is compensated in two ways: he is not charged for the parts that are not met, and moreover, he gets them for free in the next time period.
This process requires a lot of overhead for advertisers who must negotiate with sales representatives, and a lot of guess-work for sales representatives who must decide based on intuition which advertising contracts to accept. As a result, small advertisers tend to be locked out of the system, unable to bear the cost of the smallest-sized contracts, and the system overall suffers additional inefficiencies from the suboptimal decisions of the sales representatives. In this paper, we consider automating this system. We design a system which each month considers the supply of page views and a set of bids, each specifying a desired set of pages, a desired number of impressions, and a per-impression value, and then selects a subset of bids which maximizes the value while sustaining penalties for under-allocated impressions. Whereas in practice, the penalties are realized in the form of free impressions, in our system we represent these penalties with a monetary payment from the host to the advertiser equal to a specified multiple of the per-impression value for each under-allocated impression. The penalty factor reflects an estimate of how much next month's impressions are going to be worth.
There are several factors which make this system harder to design than general combinatorial allocation mechanisms. The most significant difference comes from the fact that the host must ``guarantee'' supply by paying a penalty for under-allocated impressions. Such guarantees are quite characteristic of the banner advertising market, and are important in branding campaigns where it is essential for the advertiser to receive at least some minimum number of impressions - the McDonald's arches or the Nike swoosh are recognizable precisely because they are ubiquitous. However, these guarantees also make the underlying optimization problem hard to approximate: for example, if the penalty is very large, then each winner must receive all of his requested impressions and so we can reduce our problem from the well-known set packing problem [15]. In fact, as we show, even for small penalties, our problem is not approximable within any constant factor.
We therefore focus on designing heuristics with varying sorts
of provable guarantees. A common approach to combat
inapproximability is to develop bi-criteria
approximations, or algorithms that do almost as well as the
optimum solution on a slightly harder problem. For example, in
![]() -balanced graph
partitioning, the goal is to cut the minimum number of edges to
divide a graph on
-balanced graph
partitioning, the goal is to cut the minimum number of edges to
divide a graph on ![]() vertices into
two parts, each with at most
vertices into
two parts, each with at most ![]() vertices. The seminal paper of Leighton and Rao [18] provides a bi-criteria
approximation algorithm for
vertices. The seminal paper of Leighton and Rao [18] provides a bi-criteria
approximation algorithm for ![]() -balanced graph partitioning which cuts at most a
factor of
-balanced graph partitioning which cuts at most a
factor of ![]() more edges than
the optimum solution on the harder problem of bisection, or
more edges than
the optimum solution on the harder problem of bisection, or
![]() -balanced graph
partitioning. This was improved to
-balanced graph
partitioning. This was improved to
![]() by Arora et
al. [3]. The bi-criteria
framework has also been applied to min sum clustering [5] and selfish routing [22].
by Arora et
al. [3]. The bi-criteria
framework has also been applied to min sum clustering [5] and selfish routing [22].
In our case, we apply the bi-criteria framework by designing
an algorithm that does approximately as well as the optimum
algorithm with larger penalties. Our algorithm is extremely
simple and trivial to implement: it selects at each iteration a
new winner and a corresponding set of impressions with maximum
marginal per-impression profit. We show that this algorithm gets
at least 23% of the optimum profit on a problem with ![]() times the penalty (i.e.,
whereas our algorithm just pays an advertiser his per-impression
bid for each under-allocated impression, the optimum must pay
times the penalty (i.e.,
whereas our algorithm just pays an advertiser his per-impression
bid for each under-allocated impression, the optimum must pay
![]() times the per-impression
bid).
times the per-impression
bid).
Despite the bi-criteria guarantee, we note that this greedy algorithm may perform poorly when the optimum solution has large value. These are exactly the instances in which we would like to perform well. Hence, we present a refined greedy algorithm which involves solving a flow computation and prove guarantees on its performance in the structural approximation [10] framework, a newly developed framework for evaluating the approximation factor of heuristic algorithms. This framework allows one to evaluate the approximation factor of an algorithm based on the structure of the optimal (or any) solution, and not only the value of the optimal solution. In particular, it provides a performance guarantee that improves as the performance of the optimum solution improves, and unlike the bi-criteria framework, it provides these guarantees with respect to the optimum on the same problem instance.
Our refined greedy algorithm iteratively selects advertisers with maximum marginal per-impression profit, as before, but additionally considers re-allocating impressions to already selected advertisers at each step. In evaluating this algorithm, we consider the fraction of demand that the optimum satisfies for each advertiser. We show as this fraction increases, hence increasing the optimum value, our algorithm's value also increases. For example, if the optimum always satisfies 75% of the demand of each advertiser, then our algorithm gets at least 10% of the optimum, wherease if the optimum satsifies 99% of the demand of each advertiser, then our algorithm gets at least 30% of the value of the optimum. See Section 5.1 for the exact trade-off curve.
We note that the refined greedy algorithm outperforms the simple greedy algorithm on many classes of instances. However, this improved performance comes at the expense of increased difficulty in the implementation (and an additional linear factor in the running time).
In order to model the banner advertising problems and its key feature of supply guarantees, we make several enabling assumptions. First, we assume that the supply (i.e., monthly set of page views) is known and periodic. While in reality this supply is actually unknown, it is reasonable to assume that the host has good estimates of this supply and that the supply is fairly constant over time. Furthermore, the periodic supply assumption is essential if we intend to guarantee supply to advertisers. Second, while the real goal of the host is to optimize value over time, we instead focus on optimizing on a month-by-month basis. In other words, our stated goal is to maximize value this month with no regard to the effects on following months' revenues. Hence, for example, we assume that under-allocated supply for an advertiser (which will be offered for free the following month) costs our algorithm an amount equal to the advertiser's bid. This approach works well in situations in which the monthly demand is fairly static, a reasonable assumption in banner advertising scenarios. Third, and finally,
It is important to note that we ignore incentives throughout this work, i.e., we analyze the value of our allocation mechanism in an idealized world where advertisers truthfully report their types and not in an economic equilibrium. While incentive issues are very important in practice, they tend to have less effect in highly competitive settings. In successful banner advertising systems, where lots of advertisers compete for limited supply, we intuitively expect incentives to play a minimal role. We leave it as further work to study incentives in our proposed systems and/or calculate payments to make our proposed systems truthful.
1 Related Work
The problem of maximizing welfare is a central problem in algorithmic mechanism design. This problem, even for special cases such as single-minded bidders, is known to be hard even to approximate [23,17,16,7,8]. However, under some conditions such as submodularity or subadditivity of valuations, constant-factor approximation algorithms have been developed [8,9]. For several problems with packing constraints linear programming-based and greedy constant-factor approximation algorithms have been proposed [1,13].In the context of Internet advertising, sponsored search
auctions have been studied extensively. The closest works to ours
in this literature are the ![]() -competitive algorithms that have been
designed for maximizing revenue for online allocation of
advertisement space [20,6,19].
-competitive algorithms that have been
designed for maximizing revenue for online allocation of
advertisement space [20,6,19].
Our work is distinguished from previous work in the literature by the existence of supply guarantees, implemented through penalties. These penalties reflect the non-linearity of bidder valuations, a characteristic of advertisers in banner advertising markets.
This paper is organized as follows. We give a formal definition of the model in Section 2 . In this section, we also give the following basic observation about our problem: in the guaranteed banner advertisement problem, if the set of served advertisers is fixed, the optimal allocation can be found in polynomial time. This indicates that the challenging part of the problem is to find the set of advertisers that should be served to maximize the value. In Section 3 , we prove that the problem does not admit a constant-factor approximation algorithm even for weak supply guarantee conditions. Next, in Section 4, we give a bi-criteria approximation algorithm for the problem. In Section 5, we give an adaptive greedy algorithm and analyze it in the structural approximation framework.
The banner advertisement problem can be modeled
as follows. We are given a set  of m advertisers {1,…,m} and a set
of m advertisers {1,…,m} and a set
 of advertising opportunities that can be
allocated to them. Each advertising opportunity is an impression
of an advertisement on a webpage. For the rest of the paper, we
refer to each advertising opportunity as an item. Without loss of generality, we assume all
items of
of advertising opportunities that can be
allocated to them. Each advertising opportunity is an impression
of an advertisement on a webpage. For the rest of the paper, we
refer to each advertising opportunity as an item. Without loss of generality, we assume all
items of  are distinct. The bid of an advertiser
i is a tuple (Ii,di,bi) where
Ii ⊆
are distinct. The bid of an advertiser
i is a tuple (Ii,di,bi) where
Ii ⊆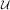 specifies the
subset of items in which advertiser i
is interested 1, di specifies the number of items the
advertiser requires, and bi
specifies the per-unit price the advertiser is willing to pay (up
to his required number of units). Allocating more than
di items to advertiser i has no marginal benefit.
specifies the
subset of items in which advertiser i
is interested 1, di specifies the number of items the
advertiser requires, and bi
specifies the per-unit price the advertiser is willing to pay (up
to his required number of units). Allocating more than
di items to advertiser i has no marginal benefit.
Following the convention of current banner advertising systems, we require our system to guarantee the supply of an advertiser. That is, by accepting the bid of advertiser i, we enter a contract for the sale of di items from the set Ii. Should we fail to fulfill this contract, we are required to pay a penalty. This penalty can be a fixed price paid for every under-allocated impressions; or more commonly, can be filled by delivering the same number of impressions for free during the following period. Both of these penalty schemes can be formalized in the following way: If the advertiser requested di units and was allocated only xi units for some xi < di, then the system collects only
in value, where λ is a fixed constant. The special case of λ = 1 can be interpreted as delivering the same number of impression for free the following month. Henceforth, we will be primarily concerned with the case λ = 1, unless otherwise stated, although all results can be appropriately generalized to other values of λ.Now we can formalize the banner advertisement
problem in the following way: Given a set of advertisers
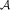 and their bids, {(Ii,di,bi)}, find a subset of advertisers, or winners, for
which accepting their bids maximizes the value. This problem is
captured by the following mathematical program. Let yi be the
indicator variable that advertiser i
is a winner; zij be the indicator variable that item
j is allocated to advertiser
i; and xi be the
total number of items allocated to advertiser i.
and their bids, {(Ii,di,bi)}, find a subset of advertisers, or winners, for
which accepting their bids maximizes the value. This problem is
captured by the following mathematical program. Let yi be the
indicator variable that advertiser i
is a winner; zij be the indicator variable that item
j is allocated to advertiser
i; and xi be the
total number of items allocated to advertiser i.
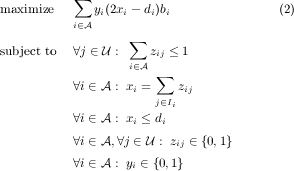
As we show in the next section, it is NP-hard to even approximate the solution of this optimization program within any constant ratio. The main difficulty comes from the multiplicative terms yixi in the objective function of the program above. However, we show that once the set of winning advertisers is determined (i.e., once we fix the {yi} variables), the resulting program can be solved combinatorially using a maximum weighted matching algorithm.
Lemma 2.1. Given the set T of winning advertisers, the problem of finding the optimum allocation of items to advertisers in T can be optimally solved in polynomial time.
 T and yi
= 0 otherwise, and by setting
xi = ∑ j
T and yi
= 0 otherwise, and by setting
xi = ∑ j Iizij. The
negative term in the resulting objective function is now a
constant, and so the problem reduces to the following program:
Iizij. The
negative term in the resulting objective function is now a
constant, and so the problem reduces to the following program:
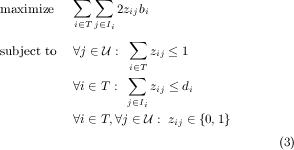
This integer program is equivalent to a maximum
weighted b-matching problem, or
f-factor problem, in which, given a
weighted graph G, the goal is to find
a maximum-weight subgraph of G in
which the degree of each node i is at
most f(i). The mapping is as follows: consider a bipartite
graph G(V,E) with node set V
(G) = 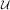 ∪ T, edge set
E(G) = {(i,j)|i
∪ T, edge set
E(G) = {(i,j)|i  T,j
T,j  Ii}, and edge
weights w(i,j) = 2bi. The
solution to the integer program is then the maximum weighted
f-matching in which f(i) = di for
i
Ii}, and edge
weights w(i,j) = 2bi. The
solution to the integer program is then the maximum weighted
f-matching in which f(i) = di for
i  T and f(j) = 1 for
j
T and f(j) = 1 for
j 
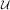 . We can
therefore use the combinatorial or LP-based algorithms for
f-matching (see, e.g.,
[]west,schrijver,BT98) to solve our problem. __
. We can
therefore use the combinatorial or LP-based algorithms for
f-matching (see, e.g.,
[]west,schrijver,BT98) to solve our problem. __
The above discussion shows that the challenging part of the banner advertising problem is to decide the set T of winning advertisers.
3. HARDNESS OF APPROXIMATION .
In this section, we show that the banner advertising problem is NP-hard to approximate within any constant ratio. In other words, for any constant 0 < c ≤ 1, it is not possible to find an allocation with value at least c times the optimum value (defined as the value of the mathematical program (2 )) in polynomial time unless P = NP.
This result is immediate for arbitrarily large penalties via a reduction from the inapproximable maximum set-packing problem []GJ79, i.e., the problem of finding the maximum number of disjoint sets in a given set family. For arbitrary penalties, we provide a reduction from the k-uniform regular set cover problem. In this problem, we are given a family of sets over a universe of elements. Each set in the family has exactly k elements, and each element in the universe is covered by exactly k sets. The goal is to select the minimum number of sets which cover all the elements. It is shown in Feige et al. []FLT04, Theorem 12, that:
Proposition
3.1. []Feige98, FLT04 For every choice of constants s0
> 0
and ε
> 0,
there exists k dependent on
ε and
instances of k-uniform regular set cover
with n elements on which it is NP-hard to distinguish between
the case in which all elements can
be covered by t = 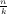 disjoint
sets, and the case in which every
s ≤
s0t
sets cover at most a fraction of 1
- (1
-
disjoint
sets, and the case in which every
s ≤
s0t
sets cover at most a fraction of 1
- (1
-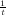 )s
+ ε of the
elements.
)s
+ ε of the
elements.
By introducing an advertiser with bid
(Ii,|Ii|, 1) for each set
Ii in the set cover instance, there is a
trivial reduction from the problem above which shows that it is
NP-hard to compute the optimum value of the banner advertising
problem. In the case in which all elements can be covered by
t =
 disjoint sets, the optimum value would be
n, but, the case in which every
s ≤
s0t sets cover at
most a fraction of 1 - (1 -
disjoint sets, the optimum value would be
n, but, the case in which every
s ≤
s0t sets cover at
most a fraction of 1 - (1 -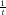 )s
+ ε of the elements, the optimum value
would be less than n.
)s
+ ε of the elements, the optimum value
would be less than n.
In order to prove hardness of approximation, we find an upper bound on the value of the optimum solution in the second case, which leads to the theorem below.
Theorem 3.2. The banner advertising problem is NP-hard to approximate within any constant ratio 0 < c ≤ 1.
The theorem is proved by showing that if one can approximate the solution within a constant ratio, then it is possible to distinguish between the instances of the set cover problem described above. The complete proof is given in appendix A. Although the proof in the appendix is presented assuming the penalty λ is equal to one, the result holds for any constant linear penalty.
In lieu of the above hardness result, we present a greedy heuristic which at each step assigns items to an advertiser that maximizes the profit-per-item. The description of the algorithm is given in Figure 1. Note that it is important to choose an advertiser that maximizes profit-per-item. The example below shows that a naive greedy algorithm which chooses the advertiser with maximum overall profit performs quite poorly even in "easy" instances.
- Example
- Suppose there are n + 1 advertisers and n items. Advertiser i, 1 ≤ i ≤ n, is interested only in item i and bids 1 for it. Advertiser n + 1 bids 1 + ε for receiving all the n items. While the optimal solution yields a value of n by allocation items 1 to n to advertisers 1 to n, the naive greedy algorithm obtains a value of just 1 + ε.
The value that algorithm greedy obtains from the instance in the previous example is equal to the optimum value.
4.1
Performance Guarantee:
Bi-Criteria
Approximation .
We analyze algorithm greedy by developing bi-criteria approximations for our problem. To do so, we compare the value of our solution to the value of the optimal solution with a greater penalty. We say an algorithm is an (α,β)-approximation if it always outputs a solution with value at least β times that of the optimal solution with (larger) penalties α. More formally, an algorithm is an (α,β)-approximation for the problem of selling banner ads if it can always obtains a β fraction of the value of the linear program below - this is the same as LP 2 but with a different objective.
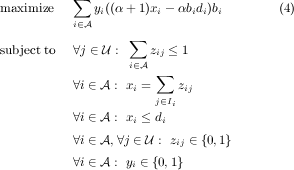
In other words, while our algorithm pays a penalty of 1 for under-allocation, the optimal solution is charged a penalty of α for some α > 1.
For algorithm greedy we can prove the following theorem:
Theorem 4.1. For α ≥ ln 2 __ 1-ln 2 ≈ 2.26, the approximation ratio of greedy algorithm is 1-ln 2 2-ln 2 ≈ 0.23. For 1 < α < ln 2 __ 1-ln 2, the approximation ratio is
where x [ α__
α+1, 1] is the root of the
equation 1∕x+(1+1∕α)
ln 2x = 2.
[ α__
α+1, 1] is the root of the
equation 1∕x+(1+1∕α)
ln 2x = 2.
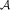 be the set of all advertisers who contribute
a positive profit to optα.
For i
be the set of all advertisers who contribute
a positive profit to optα.
For i 
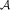 , let
Si be the set optα allocated to advertiser
i. To simplify notation, we use
si to denote
, let
Si be the set optα allocated to advertiser
i. To simplify notation, we use
si to denote 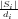 . Without loss of
generality, we may assume α __
α+1
< si ≤
1.
. Without loss of
generality, we may assume α __
α+1
< si ≤
1.
In the analysis of greedy algorithm, we will partition each item into two subitems: the P subitem that takes up a p fraction of the item, and the Q subitem that takes up a (1 - p) fraction of the item; we will determine the value of p later. We will develop lower bounds on the profit of greedy by a case analysis. In each case, we will compare the profit optα gets to one of two kinds of profit that greedy gets: only to the part computed over P subitems, or only to the part computed over Q subitems. Summing over all advertisers, the P part and Q part of each item, and hence the whole item, is counted at most once.
For i 
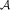 , there are two cases:
, there are two cases:
-
greedy
allocates strictly less than |Si|-⌈di∕2⌉ items
from Si. In this case we consider the profit
greedy
obtains from P subitems assigned
to i.
When j elements of Si are remaining, greedy could allocate these elements to i with profit-per-item 2j-di____ j bi. This profit is positive for ⌈di∕2⌉ < j ≤|Si|. Therefore, in this case, greedy must have allocated a nonempty set to advertiser i since otherwise greedy could get positive per-item profit by adding i to the solution and allocating the unallocated items of Si to i. Furthermore, as greedy has items of Si available when assigning items to i, it follows that the demand di of advertiser i is fully satisfied. Hence greedy gets complete profit for P subitems, giving a profit of pdibi.
-
greedy
allocates at least |Si|-⌈di∕2⌉ items
from Si In this case we consider the profit
greedy
gets from Q subitems of
Si.
Note, greedy must have obtained a profit of at least 2j-di____ j bi from the (|Si|- j + 1)'th item allocated from Si as this is the per-item profit greedy obtains by allocating the remainder of Si to i. Summing over j, ⌊di∕2⌋ + 1 ≤ j ≤ |Si|, greedy must have allocated these items with total profit at least:
Taking into account that this profit comes only from the Q part of items, this gives a profit of (1 - p)(2si - 1 - ln 2si)dibi.
For each advertiser i, exactly one of the above cases happens. Furthermore, for each item, the P part is counted at most once since the assignment in case 1 is a subset of the solution for greedy and hence disjoint. Similarly, the Q part is also counted at most once since the Si considered in case 2 is a subset of the optimum solution and hence disjoint. Therefore, we have shown that greedy gets a profit of at least:
The profit of optα from Si is ((α + 1)si -α)dibi. Therefore, the ratio of the profit of greedy to optα is at least min{p, (1 -p)γ}, where γ is defined as Choosing p = γ __ 1+γ gives the approximation ratio γ __ 1+γ .We find a lower bound on γ using the first and second order conditions. The details of calculations are given in appendix B. For α ≥ ln 2 __ 1-ln 2, γ takes its minimum for si = 1. Plugging in (8), we get γ = 2-1-ln 2 _ (α+1)si-α = 1 - ln 2 and p = 1-ln 2 2-ln 2
For 1 < α < ln 2 __ 1-ln 2, as we prove in appendix B, there exists a point x in [ α__ α+1, 1] for which si = x gives the minimum value of γ. This point is the root of the equation below which is derived by taking the derivatives of (8):
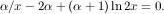
We give an example which shows the analysis is tight for α ≥ ln 2 __ 1-ln 2. In this example, the optimal solution allocates all of the items to the advertisers without paying any penalty. However, the greedy algorithm obtains just a 1-ln 2 2-ln 2 fraction of the optimal solution.
- Example
-
Assume for an even number k,
there are m = 3k∕2
advertisers and km items. Suppose
these items are represented by an m �/span> k matrix C. Each
advertiser has a demand of k
items. Advertiser i, 1 ≤
i ≤ k, is only
interested in items in row i,
i.e. {cij|1 ≤ j
≤ k}, and bids
1 for each of these items.
Advertiser i, k+1 ≤ i
≤ 3k∕2, bids
2-
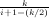 for
each item in row i. He also bids
2 -
for
each item in row i. He also bids
2 -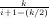 for
each item in column i
- k∕2.
for
each item in column i
- k∕2.
By induction, one can show that at step j, for 1 ≤ j ≤ k∕2, greedy may allocate the top k items in column k - j + 1, to advertiser 3k∕2 -j + 1. Therefore, the total profit of greedy is:
We can make k arbitrary large. Hence, profit of greedy can be approximated by k2(1 - ln 2), with arbitrary high accuracy: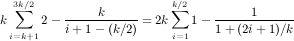 The optimal solution gives advertiser i, 1 ≤ i ≤ m, all the items in row i. Hence, it gets a profit k2 from the first k advertiser and a profit k2(1 - ln 2) from the rest. Therefore, the approximation ratio of greedy is bounded by 1-ln 2 2-ln 2.
The optimal solution gives advertiser i, 1 ≤ i ≤ m, all the items in row i. Hence, it gets a profit k2 from the first k advertiser and a profit k2(1 - ln 2) from the rest. Therefore, the approximation ratio of greedy is bounded by 1-ln 2 2-ln 2.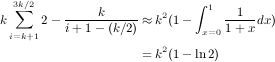
5. AN ADAPTIVE GREEDY ALGORITHM .
As suggested by Example 4.1 , fixing the items allocated to each advertiser may hurt the performance of the algorithm. In this section, we give an adaptive greedy algorithm called adaptive greedy. Similar to the previous greedy algorithm, this algorithm iteratively selects new winners. However, in each iteration, it fixes only the number of items assigned to the new winner and not the precise set of items. This flexibility allows adaptive greedy to find the optimum solution in Example 4.1 and, as we will show, allows us to prove better approximation guarantees in general.
We use the following notation throughout this
section. For a winning advertiser i,
let ci be the number of items allocated to
i. Note as mentioned above that
ci remains fixed although the set of
allocated items may change throughout the course of the
algorithm. Let Gt be the set of advertisers chosen by the
algorithm up to but not including time t. For j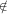 Gt, let fjt be the
maximum number of items that we could allocate to advertiser
j, subject to the constraint that
each advertiser i
Gt, let fjt be the
maximum number of items that we could allocate to advertiser
j, subject to the constraint that
each advertiser i  Gt gets
exactly ci items. More formally, fjt is the
solution of the following integer program.
Gt gets
exactly ci items. More formally, fjt is the
solution of the following integer program.
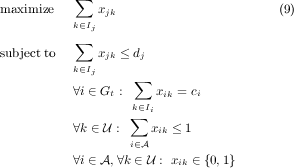
Also, let rjt
= 2fjt-dj
fjt ⋅
bj be the maximum per-item profit that we
could obtain from advertiser j,
subject to the constraints. At step t, algorithm adaptive
greedy
chooses the advertiser with maximum rjt,
j Gt. The
algorithm is given in Figure 5
.
Gt. The
algorithm is given in Figure 5
.
To compute fjt, one can solve the linear relaxation of the above program and round the solution to an integer solution (without decreasing the objective function). For a complete description of the algorithm, we refer the reader to []BT98. 2
5.1
Performance Guarantee:
Structural
Approximation .
As we observed in Section 3 , the hardness result implies that we do not hope to analyze the adaptive greedy algorithm by the traditional multiplicative approximation framework. However, in order to distinguish the quality of different algorithms in practice, we can use other approximation measures such as the bi-criteria approximation.
In this section, we analyze the adaptive greedy algorithm using a newly defined framework for evaluating heuristics called structural approximation []FIMN08. The main feature of this framework is that it is designed to evaluate the approximation ratio of an algorithm based on the structure of an optimal (or any) solution, and not only the value of an optimal solution. In this framework, given a solution with some value, we define the recoverable value of the solution based on its structure. The goal is to show that the value of our algorithm is at least as much as the the recoverable value of any solution. 3 We would like to design a recoverable value function that is very close to the real value. Note that in the traditional multiplicative approximation framework, the recoverable value is restricted to a multiplicative ratio of the value of the solution. By allowing more general functions for the recoverable value, the structural approximation framework is more flexible, and therefore can distinguish among different algorithms with the same worst-case multiplicative approximation guarantees. Additionally, this framework provides a way for comparing the quality of our solution to that of the optimal solution of the same problem (with the same parameters). This is in contrast to the bi-criteria approximation framework in which we compare the value of our solution to the value of a problem with different parameters. We refer the reader to []FIMN08 for a more detailed discussion of the structural approximation framework.
We now analyze adaptive
greedy
algorithm using the structural approximation framework. Let
 be the set of advertisers that are allocated
a non-empty set in the optimal solution, i.e., the winners. For
each advertiser i
be the set of advertisers that are allocated
a non-empty set in the optimal solution, i.e., the winners. For
each advertiser i 
 , let Si be the
set of items allocated to i in an
optimal solution. For i ⁄
, let Si be the
set of items allocated to i in an
optimal solution. For i ⁄
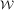 , Si is
taken to be the empty set. Let si
= |Si| di . Then
the value of the optimal solution is: ∑ i
, Si is
taken to be the empty set. Let si
= |Si| di . Then
the value of the optimal solution is: ∑ i
 (2si -
1)dibi. We
define
(2si -
1)dibi. We
define
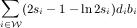
Theorem 5.1. Let Si be the set of items assigned to advertiser i by an optimal solution. Also, let si = |Si| di . adaptive greedy algorithm obtains a value of at least:
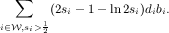
Corollary 5.1. Consider a collection {(qi,αi)} corresponding to an optimal solution, where qi is the fraction of the value of the solution comes from the advertisers for which an αi fraction of the demand is satisfied. Then, the approximation ratio of adaptive greedy is at least:
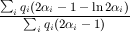
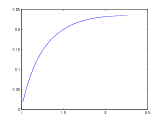
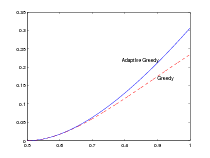
In particular, when in the optimal solution, at least an s fraction of the demand of all winning advertisers is satisfied, adaptive greedy obtains at least a fraction (2s- 1 - ln 2s) of the value of the optimal solution. Figure 4 depicts this lower bound on the value for 1 2 ≤ s ≤ 1.
|
|
Proof. To prove Theorem 5.1 , without loss of generality, we assume the algorithm chooses advertisers 1, 2,…,T in order. We inductively construct a sequence of assignments of items to advertisers which we call canonical assignments. Let
 0 be the
empty set. The t-th element of the
sequence of assignments, denoted by
0 be the
empty set. The t-th element of the
sequence of assignments, denoted by  t, is
an assignment of items to advertisers 1,…,t which
satisfies the following properties.
t, is
an assignment of items to advertisers 1,…,t which
satisfies the following properties.
- Each advertiser i, 1 ≤ i ≤ t, is assigned exactly ci items.
- All items that are assigned in
 t-1 are also assigned in
t-1 are also assigned in  t,
i.e. are assigned to advertisers 1,…,t.
t,
i.e. are assigned to advertisers 1,…,t. - For each advertiser i, 1 ≤ i ≤ t, all the
items in Si (namely, the items allocated to
i by the optimal solution, if
i

 ) are assigned.
(This property trivially holds for i ⁄
) are assigned.
(This property trivially holds for i ⁄
 .)
.)
In the following lemma, we show that such a sequence of assignments exists.
Lemma
5.1. There exists a sequence
{ 1,
1, 2,…,
2,…, t}
of canonical
assignments which satisfies the properties above.
t}
of canonical
assignments which satisfies the properties above.

 . In this case we observe that
c1 ≥|S1|, and hence a
canonical assignment exists. Therefore, the base of induction
holds.
. In this case we observe that
c1 ≥|S1|, and hence a
canonical assignment exists. Therefore, the base of induction
holds.
Now consider t >
1. Assume a sequence of canonical
assignments  1,…,
1,…, t-1, and let
t-1, and let
 t be an
optimal solution for LP (9
). We change
t be an
optimal solution for LP (9
). We change  t to a
canonical assignment satisfying the above three properties. For
1 ≤
i < t, let Bi be the
set of item that are assigned to advertiser i in
t to a
canonical assignment satisfying the above three properties. For
1 ≤
i < t, let Bi be the
set of item that are assigned to advertiser i in  t-1. Also, let Bt the set
of items in St that are not assigned to any advertiser
in
t-1. Also, let Bt the set
of items in St that are not assigned to any advertiser
in  t-1. Note that
|Bt|≤
ct, because if we assign each item in
Bi, 1
≤ i
≤ t,
to advertiser i, it gives us a
feasible solution of LP (9
).
t-1. Note that
|Bt|≤
ct, because if we assign each item in
Bi, 1
≤ i
≤ t,
to advertiser i, it gives us a
feasible solution of LP (9
).
We repeat the following procedure as long as
there exists an item x such that
x  Bi, for an advertiser 1 ≤ i ≤ t, and x is not
assigned to any advertisers in
Bi, for an advertiser 1 ≤ i ≤ t, and x is not
assigned to any advertisers in  t. Since advertiser i has received ci items
in
t. Since advertiser i has received ci items
in  t, and
|Bi|≤
ci, there exists an item y
t, and
|Bi|≤
ci, there exists an item y Bi that is
assigned to i in
Bi that is
assigned to i in  t. We
update
t. We
update  t
by assigning x to i and removing y from
the set of items allocated to i. Note
that each time we perform the procedure, the number of items that
is allocated to each advertiser remains the same. However, the
number of items that are allocated to the same advertisers in
t
by assigning x to i and removing y from
the set of items allocated to i. Note
that each time we perform the procedure, the number of items that
is allocated to each advertiser remains the same. However, the
number of items that are allocated to the same advertisers in
 t and
the assignment defined by Bi's
increases by 1. Since the number of items that are allocated to
the same advertiser in
t and
the assignment defined by Bi's
increases by 1. Since the number of items that are allocated to
the same advertiser in  t and the assignment defined by
Bi's is at most ∑ 1≤i≤tci, after
some number of steps, we reach a point where no such update is
possible. Therefore, the final assignment after these set of
updates satisfies all the three properties. __
t and the assignment defined by
Bi's is at most ∑ 1≤i≤tci, after
some number of steps, we reach a point where no such update is
possible. Therefore, the final assignment after these set of
updates satisfies all the three properties. __
Now we are ready to prove Theorem 5.1. Note that the
value obtained from each assignment only depends on the number of
items allocated to each advertiser. Therefore, without loss of
generality, we might assume that adaptive
greedy
allocates to each advertiser the same set of items assigned to
this advertiser in canonical assignment  T.
T.
For i 
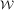 , let kit be the
number of items of Si that are not assigned in
, let kit be the
number of items of Si that are not assigned in  t-1. Since we can
construct a feasible solution with value kit for LP
(9) using
t-1. Since we can
construct a feasible solution with value kit for LP
(9) using
 t-1, we observe
that fit ≥
kit. Therefore, the value-per-item that
adaptive
greedy
would obtain at this point if it chooses advertiser i and assigns to it all not previously assigned
items of Si at least (2
- di _
kit)bi. Thus,
the value adaptive
greedy
obtains by the end of the algorithm is at least:
t-1, we observe
that fit ≥
kit. Therefore, the value-per-item that
adaptive
greedy
would obtain at this point if it chooses advertiser i and assigns to it all not previously assigned
items of Si at least (2
- di _
kit)bi. Thus,
the value adaptive
greedy
obtains by the end of the algorithm is at least:
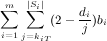
For i 
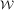 , if advertiser i
is chosen by adaptive
greedy
then kiT = 0, and if
advertiser i is not chosen by
adaptive
greedy
then necessarily kiT ≤
di 2 .
Therefore:
, if advertiser i
is chosen by adaptive
greedy
then kiT = 0, and if
advertiser i is not chosen by
adaptive
greedy
then necessarily kiT ≤
di 2 .
Therefore:
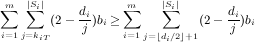
By the same calculation as in Theorem 4.1, equation (6), the value obtained by adaptive greedy is at least:
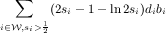
Note that while we stated all our results with respect to the recoverable value of an optimal solution, our proofs in fact follow when considering the recoverable value of any solution.
5.2 Comparison of GREEDY and ADAPTIVE GREEDY .
We analyzed adaptive greedy algorithm using the structural approximation framework. We also analyzed the greedy algorithm using the bi-criteria approximation framework. In order the compare these two greedy algorithms, we now analyze the greedy algorithm in the structural approximation framework.
Let 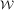 be the set of
the winners in an optimum solution (or any feasible solution).
Assume that this solution satisfies a si
fraction of the demand of advertiser i
be the set of
the winners in an optimum solution (or any feasible solution).
Assume that this solution satisfies a si
fraction of the demand of advertiser i 
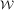 . Note that si
≥ 1
2, i
. Note that si
≥ 1
2, i

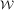 . By equation (7
), in the proof of Theorem
4.1, for any
p, 0
≤ p
≤ 1,
greedy
obtains a value of at least:
. By equation (7
), in the proof of Theorem
4.1, for any
p, 0
≤ p
≤ 1,
greedy
obtains a value of at least:
Given si's, one can compute the value of p which maximizes the sum and gives a recoverable value for each solution. However, by Theorem 5.1 , the value of adaptive greedy algorithm from the same instance is at least:
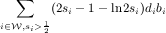
This immediately shows that adaptive greedy gives us a better guarantee on the value of the solution.
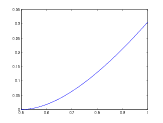
When in an optimum solution, fraction s of the demand of all advertisers is satisfied, we can easily compare the guarantees on the value given in Theorems 4.1 and 5.1 . In this case, the optimum value for p in (10) is equal to 2s-1-ln 2s 2s-ln 2s , which leads to the same guarantee on the approximation ratio of greedy algorithm. The guarantee on the approximation ratio of adaptive greedy algorithm is 2s - 1 - ln 2s. Figure 5 depicts these guarantees on the approximation ratio for 1_ 2 ≤ s ≤ 1.
|
|
One way to see that adaptive greedy strictly outperforms greedy is to observe that adaptive greedy algorithm obtains the optimum value of the instance described in Example 4.1. As a result, the ratio between the values of the solutions obtained by these two algorithms is 2 - ln 2.
In this paper we showed that having supply guarantees makes the problem of maximizing the value of selling banner advertisements inapproximable. In the lieu of this hardness result, we proposed two greedy heuristics for the banner advertising problem and analyzed them rigorously in the bi-criteria and structural approximation frameworks. Given the simple and flexible nature of these algorithms, we expect that these algorithms can help in automating the negotiation process for banner advertising.
In order to make our algorithms even more applicable to practical settings, we would like to consider the online or stochastic settings, in which advertisers arrive over time and submit bids which must be immediately accepted or rejected, without knowledge of exact future demand. Also along these lines, it would also be useful to relax the assumption that the supply of items is known a priori. In practice, hosts have good estimates of the number of page views. However, these estimates may have large variance, and we should ideally provide algorithms which are robust with respect to errors in the supply estimates. Finally, to completely automate the banner advertising process and replace it with a repeated auction mechanism, it is necessary to design a pricing mechanism to accompany our allocation mechanism and analyze the resulting incentives.
Bibliography
- 1
- G. Aggarwal and J. D. Hartline,
Knapsack Auctions,
Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), 2006. - 2
- G. Ausiello, A. D'Atri, and M. Protasi.
Structure Preserving Reductions Among Convex Optimization Problems.
Journal of Computer and System Sciences, 21, 136-153, 1980. - 3
- S. Arora, S. Rao, and U. Vazirani.
Expander Flows, Geometric Embeddings, and Graph Partitionings.
Proceedings of 36th Annual Symposium on the Theory of Computing (STOC), 222-231, 2004. - 4
- D. Bertsimas and J. Tsitsiklis.
Introduction to Linear Optimization.
IIE Transactions, 1998. - 5
- Y. Bartal, M. Charikar, and D. Raz,
Approximating Min-Sum k-Clustering in Metric Spaces,
Proceedings of the 33rd Annual ACM Symposium on Theory of Computing (STOC), 2001. - 6
- Niv Buchbinder, Kamal Jain, and Seffi Naor.
Online Primal-Dual Algorithms for Maximizing Ad-Auctions Revenue.
Proceedings of the 15th Annual European Symposium on Algorithms (ESA), 2007. - 7
- P. Cramton, Y. Shoham, and R. Steinberg.f
Combinatorial Auctions.
MIT Press, Cambridge, MA, 2005. - 8
- S. Dobzinski, M. Schapira, and N. Nisan
Truthful Randomized Mechanisms for Combinatorial Auctions.
Proceedings of the 38rd Annual ACM Symposium on Theory of Computing (STOC), 2006. - 9
- U. Feige.
On Maximizing Welfare When Utility Functions Are Subadditive.
Proceedings of the 38rd Annual ACM Symposium on Theory of Computing (STOC), 2006. - 10
- U. Feige, N. Immorlica, V. Mirrokni, and H.
Nazerzadeh.
Structural Approximations - a framework for analyzing and designing heuristics.
manuscrip. - 11
- U. Feige.
A Threshold of ln n for Approximating Set Cover.
Journal of ACM, 45(4):634-652, 1998 - 12
- U. Feige, V. Mirrokni, and J. Vondrak.
Maximizing Non-Monotone Submodular Functions.
Proceedings of 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS), 2007. - 13
- L. Fleischer, M. Goemans, V. Mirrokni, and M.
Sviridenko.
Tight Approximation Algorithms for Maximum General Assignment Problems.
Symposium of Discrete Algorithms (SODA), 2006. - 14
- U. Feige, L. Lov
 sz
and P. Tetali,
sz
and P. Tetali,
Approximating Min Sum Set Cover,
Algorithmica 40(4): 219-234, 2004. - 15
- M. Garey and D. Johnson.
Computers and Intractability: A Guide to the Theory of NP-Completeness.
WH Freeman Co
New York, 1979.
Co
New York, 1979. - 16
- B. Lehmann, D. Lehmann, and N. Nisan.
Combinatorial Auctions with Decreasing Marginal Utilities.
Proceedings 3rd ACM Conference on Electronic Commerce (EC), 2001. - 17
- D. J. Lehmann, L. O'Callaghan, and Y. Shoham.
Truth revelation in approximately efficient combinatorial auctions.
J. ACM, 49(5), 577-602, 2002. - 18
- F. T. Leighton and S. Rao.
An Approximate Max-Flow Min-Cut Theorem For Uniform Multicommodity Flow Problems with Applications to Approximation Algorithms.
Proceedings of 29th Annual Symposium on Foundations of Computer Science, pages 422-431, 1988. - 19
- M. Mahdian, H. Nazerzadeh, and A. Saberi
Allocating Online Advertisement Space with Unreliable Estimates
Proceedings 8th ACM Conference on Electronic Commerce (EC), 2007. - 20
- A. Mehta, A. Saberi, U. Vazirani, and V. Vazirani.
AdWords and Generalized Online Matching.
Journal of the ACM, Volume 54 , Issue 5, 2007. - 21
- Pricewaterhouse Coopers LLP.
IAB Internet Advertising Revenue Report.
http://www.iab.net/resources/adrevenue/pdf/IAB_PwC
_2006_Final.pdf - 22
- T. Roughgarden and �. Tardos.
How Bad is Selfish Routing?.
Proceedings of IEEE Symposium on Foundations of Computer Science, 93-102, 2000. - 23
- T. Sandholm.
Algorithm for Optimal Winner Determination in Combinatorial Auctions.
Artificial Intelligence, 135:1-54, 2002. - 24
- A. Schrijver.
Combinatorial Optimization.
Springer, 2003. - 25
- D. B. West.
Introduction to Graph Theory.
Prentice Hall, 2001.
APPENDIX
A.
PROOF OF THEOREM 3.2
. Proof.
We prove that claim holds even if the advertisers have large
demands. We define a special case of selling banner
advertisements . Consider m sets
A1,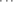 ,Am, each of size k; let A = ∪i=1mAi and
n =
|A|. Also consider a
set Q of size q which is disjoint from A. Also, assume k
= O(q) and kq = o(
,Am, each of size k; let A = ∪i=1mAi and
n =
|A|. Also consider a
set Q of size q which is disjoint from A. Also, assume k
= O(q) and kq = o(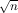 ).
).
Problem 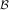 (k,q,n) is defined with m
advertisers. Let c = 2(1 -
(k,q,n) is defined with m
advertisers. Let c = 2(1 -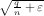 ). Let the bid of advertiser
i, (Ii,di,bi), be equal to
(Q
∪ Ai,ck,
1). We show that it is NP-Hard to
approximate
). Let the bid of advertiser
i, (Ii,di,bi), be equal to
(Q
∪ Ai,ck,
1). We show that it is NP-Hard to
approximate  (k,q,n) within a ratio
of 2
(k,q,n) within a ratio
of 2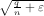 .
.
Consider the k-uniform regular set
cover instances defined in the proposition 3.1
, for ε and s0
= 3. We say an instance is of type YES
if all elements can be covered by t
disjoint sets. An instance is of type NO if every s ≤ s0t sets cover at
most a fraction of 1 - (1 -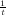 )s
+ ε of the elements. We show if an
algorithm can approximate problem
)s
+ ε of the elements. We show if an
algorithm can approximate problem 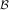 (k,q,n) within a ratio of 2
(k,q,n) within a ratio of 2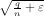 , then this algorithm can
distinguishes between YES and NO instances.
, then this algorithm can
distinguishes between YES and NO instances.
For the YES instances, there are t =  disjoint set which cover all the n
elements. Hence, the value in this case is at least t(k - (kc - k)) = n(2 - c).
disjoint set which cover all the n
elements. Hence, the value in this case is at least t(k - (kc - k)) = n(2 - c).
For a NO instance, any s sets, 0 ≤ s ≤ s0t, cover at
most q +
(1 - (1 -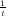 )s + ε)n elements. Therefore, the value of any
s sets is at most 2(q + (1 - (1 -
)s + ε)n elements. Therefore, the value of any
s sets is at most 2(q + (1 - (1 -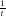 )s + ε)n) -csk. Note that
t can be made arbitrary large
([]FLT04); hence, we can approximate (1 -
)s + ε)n) -csk. Note that
t can be made arbitrary large
([]FLT04); hence, we can approximate (1 -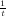 ) with e
) with e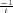 with arbitrary accuracy.
Thus, the value of any s sets is at
most:
with arbitrary accuracy.
Thus, the value of any s sets is at
most:
We find the optimum value for s by the first order conditions:
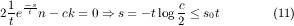
Plugging s
= -t log 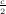 in (11
), the maximum value is at
most 2(q
+ (1 -
in (11
), the maximum value is at
most 2(q
+ (1 -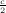 +
ε)n) + cn log
+
ε)n) + cn log 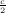 . Note that the value for any choice of
m ≥
s0t sets is
negative, because the total demand is more than double of the
number of elements. Therefore, the ratio between the value from a
NO instance and a Yes instance is at most:
. Note that the value for any choice of
m ≥
s0t sets is
negative, because the total demand is more than double of the
number of elements. Therefore, the ratio between the value from a
NO instance and a Yes instance is at most:
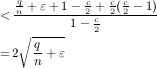
Recall that 1
-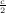 =
=
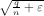 , which completes the proof. __
, which completes the proof. __
B. FINDING A LOWER BOUND ON γ .
Here, we compute a lower bound on the value of γ defined in (8). Taking the derivative of 2si-1-ln 2si (α+1)si-α with respect to si:
Define fα(x) = α∕x
- 2α + (α
+ 1) ln
2x,x
 (0, 1]. The first and
the second derivative of fα
with respect to x are:
(0, 1]. The first and
the second derivative of fα
with respect to x are:
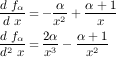
Hence, for α
> 1 and x  (0, 1], function fα
is strictly convex and takes its minimum at x = α __ α+1. Therefore,
fα is increasing in [ α__
α+1, 1].
(0, 1], function fα
is strictly convex and takes its minimum at x = α __ α+1. Therefore,
fα is increasing in [ α__
α+1, 1].
If fα(1) = ln 2 - (1 - ln 2)α ≤ 0, then fα is negative in [ α__ α+1, 1]. Hence, (12 ) is decreasing in [ α__ α+1, 1], and take its minimum at 1. For α ≥ ln 2 __ 1-ln 2, fα(1) ≤ 0. Plugging in (8 ), γ = 2-1-ln 2 _ (α+1)si-α = 1 - ln 2. Therefore, for this range of α, the approximation ratio is 1-ln 2 2-ln 2.
For 1 < α < ln 2 __ 1-ln 2, as we prove later, fα( α__ α+1) is negative. Because fα(1) is positive, by the intermediate value theorem, there exists a point x* in [ α__ α+1, 1] for which fα is zero. This point is the root of equation:
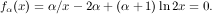
Because fα is increasing in [ α__ α+1, 1], by convexity, x* gives the minimum value of (12 ). Plugging this value for γ into γ __ 1+γ , we get (5) as a lower bound on the approximation ratio of 1 < α < ln 2 __ 1-ln 2.
Now we only need to show that for α > 1, fα( α__ α+1) is negative. For x = 1 2, fα(1 2) = 2α - 2α + (α + 1) ln 1 = 0. Also, fα is strictly convex and takes its minimum at α __ α+1 > 1 2. Therefore, fα( α__ α+1) < 0.