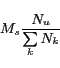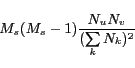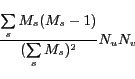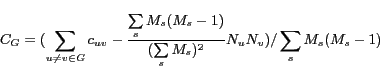1 Introduction
People have been using virtual communities to communicate since the beginning of the Internet. In the last few years, many virtual communities burgeon on the Internet, and it is very easy now to build a new virtual community using tools provided by those web-based community building sites. In simple terms, virtual community (or online community) is the gathering of people, in online space where they can come, communicate, and get to know each other better over time. According to the definition of Howard Rheingold in [3], virtual communities are social aggregations that emerge from the Net when enough people carry on public discussions long enough, with sufficient human feeling, to form webs of personal relationships in cyberspace.An important feature of the virtual community is the open membership. One can join any virtual community he want, and he can reach all its members easily. The open access to virtual communities brings numerous members to them. But among those members, most are seldom heard to other members. Among those non-active members, some are pure observers, and some are light participants, raising voice occasionally. Only a small portion of the members are active in the virtual community. In our study, such active members are called core members.
Finding the core members in virtual community is an intriguing problem and has been little researched so far. In this paper, inspired by the ideas of Guimera[1] we proposed a computer algorithm to solve this problem. As an example, we give results from the application of this algorithm in the virtual communities of a Chinese web site Douban.com.
2 The Algorithm
According to our intuitive understanding and the definition by Rheingold[3], the shared interests and activities are one of the most important feature of the virtual community. Generally, the shared interests and activities are the major reason to attract users to join the virtual community.In most of the virtual community web sites, the user tagging
information can be used to define the interests of the users. We
assume that one user u's interests can be presented by the
set of subjects which have been tagged by this user. So user
u has a set of tagged subjects:
![]() .
As a result, we can get a bi-partite graph between all users and
tagged subjects.
.
As a result, we can get a bi-partite graph between all users and
tagged subjects.
Considering user ![]() and subject
and subject
![]() : assuming that
: assuming that ![]() has been tagged by
has been tagged by ![]() users, and user
users, and user ![]() has
tagged
has
tagged ![]() subjects, then, the
probability that user
subjects, then, the
probability that user ![]() have tagged
have tagged
![]() is:
is:
So, it can be easy to know the probability that ![]() has been tagged by both
has been tagged by both
![]() and
and ![]() is:
is:
The expectation of the number of subjects tagged by both
![]() and
and ![]() is (note that
is (note that
![]() ):
):
As
![]() and
and
![]() are global
properties which do not depend on the pair of
are global
properties which do not depend on the pair of ![]() and
and ![]() selected, we
can calculate equation (3) very quickly using
some simple multiply operations. So given a user set
selected, we
can calculate equation (3) very quickly using
some simple multiply operations. So given a user set
![]() , we
can define the user interests concentration ratio as the
cumulative deviation of the number of shared subjects tagged from
the random expectation:
, we
can define the user interests concentration ratio as the
cumulative deviation of the number of shared subjects tagged from
the random expectation:
where ![]() is the number of
shared interests tagged by both
is the number of
shared interests tagged by both ![]() and
and ![]() . If the number of shared
interests in group
. If the number of shared
interests in group ![]() is no
different from the random expectation, then this quantity
is no
different from the random expectation, then this quantity
![]() will be zero. If the value
will be zero. If the value
![]() is larger than zero, it
indicates that the users in group
is larger than zero, it
indicates that the users in group ![]() have more shared interests than the random expectation.
have more shared interests than the random expectation.
In a virtual community, the core members will have more
interaction with each other than those non-core members. As a
result, the core members in a virtual community would share more
common interests with each other than those non-core members. So
we can use the user interest concentration ratio ![]() to find the core members in virtual communities:
the problem of finding the core members of a virtual community
can be transformed into the problem of finding the portion of
members in the virtual community with large
to find the core members in virtual communities:
the problem of finding the core members of a virtual community
can be transformed into the problem of finding the portion of
members in the virtual community with large ![]() value.
value.
In order to solve this problem, we choose to use the simulated annealing (SA)[2] method. Simulated annealing[2] is a stochastic optimization technique that enables one to find `low cost' configuration without getting trapped by the `high cost' local minima.
Our algorithm can now be defined as follows.
- Set the initial temperature as
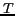 and initial solution
and initial solution  ;
; - Randomly choose
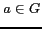 : if
: if
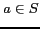 , then
, then
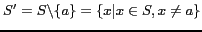 ;
if
;
if 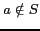 ,
,
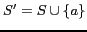 ;
; - Calculate
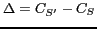 :
if
:
if 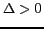 , accept the new
solution
, accept the new
solution 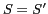 , if
, if
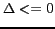 , accept the
new solution
, accept the
new solution 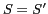 with the
probability
with the
probability
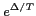 ;
; - Cool down the temperature
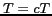 , c=0.995;
, c=0.995; - Repeat step 2 - 4 until the temperature
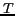 is small enough.
is small enough.
3 Results on Douban.com
In order to test our algorithm, here we give one example, the analysis of the virtual communities in Douban.com. Douban.com is a Chinese web site. It can be labeled as a ``collaborative filtering'' or ``collaborative tagging'' site, where one can tag his interested items and share his reviews or comments about millions of books and movies with others. Basing on the user-tagging behaviors, reviews and comments, Douban.com helps its users to get recommendations about new books and movies.As another result, Douban.com can also help one to find other users with similar tastes and interests, so they can get connected and communicate with each other. Douban.com provide a community service, which is called ``Douban Group''. Anyone can set up a new group about some topic and invite others to join this group. In these groups, group members can discuss their interested topic, and get more information from other members.
In this study, we chose all tagged items by one user as his interests profile. Each item which has been tagged by a user is one of his interests. Our algorithm can output a list of core members for each group.
Since there was no explicit core members data in Douban.com, we needed to use human raters to generate ``gold standard'' to evaluate our results. As it was not possible for us to rate a large number of groups and users, we rate only a small set of the users. We randomly chose 10 middle-sized groups (group size varies from 100 to 200) from 38423 groups on Douban.com, and then for each group, 20 members were chosen as our evaluation samples.
We invited two raters who are also Douban.com users(but not
the members of the 10 selected group). For each group, the raters
explored the group's home page, bulletin boards and personal
profiles of every members, so as to decide weather the 20
selected user was the core member of the group. Users were
categorized as Table 1.
After both raters submit the rating results, we use the average score by the two rater as the final human rating results. Table 2 shows the correlation between human rating score and the algorithm output score for all of our 200 test samples. This results show that our algorithm can find most of the core members from the virtual community, although the false positive rate is quite high.