Measuring Extremal Dependencies in Web Graphs

Yana Volkovich

University of Twente
Enschede, The Netherlands

Nelly Litvak

University of Twente
Enschede, The Netherlands

Bert Zwart

Georgia Tech.
Atlanta, Georgia, USA

Copyright is held by the World Wide Web Conference Committee (IW3C2). Distribution of these papers is limited to classroom use, and personal use by others.
WWW 2008, April 21-25, 2008, Beijing, China.
ACM ???.

ABSTRACT

We analyze dependencies in power law graph data (Web sample, Wikipedia sample and a preferential attachment graph) using statistical inference for multivariate regular variation. The well developed theory of regular variation is widely applied in extreme value theory, telecommunications and mathematical finance, and it provides a natural mathematical formalism for analyzing dependencies between variables with power laws. However, most of the proposed methods have never been used in the Web graph data mining. The present work fills this gap. The new insights this yields are striking: the three above-mentioned data sets are shown to have a totally different dependence structure between different graph parameters, such as in-degree and PageRank.

Categories & Subject Descriptors

{E.1}[Data structures] Graphs and networks; {G.3}[Probability and Statistics] Multivariate statistics

General Terms

Algorithms, Experimentation, Measurement

Keywords

Regular variation, PageRank, Web, Wikipedia, Preferential attachment


1 Introduction

The question of measuring correlations in the Web data has led to many controversial results. Most notably, there is no agreement in the literature on the dependence between in-degree and PageRank of a Web page [4], [5]. One of the main points that we make in this work is that the commonly used correlation coefficient is an uninformative dependence measure in heavy-tailed data [3], [7] typical for the Web and Wikipedia graphs.

A natural mathematical formalism for analyzing power laws is provided by the theory of regular variation. By definition, the distribution $ F$ has a regularly varying tail with index $ \alpha$, if $ {\mathbb{P}}(X>x)=x^{-\alpha}L(x),\;x>0,$ where $ L(x)$ is a slowly varying function, that is, for $ x>0$, $ L(tx)/L(t)\to 1$ as $ t\to\infty$. Below we analyze the dependence structure in the power law data by means of contemporary statistical techniques specially designed for multivariate regular variation [7].


2 Data Sets

We chose three data sets that represent different network structures. As the Web sample, we used the EU-2005 data set with $ 862.664$ nodes and $ 19.235.140$ links, that was collected by LAW [1]. We also performed experiments on the Wikipedia(En) graph, that contains $ 4.881.983$ nodes and $ 42.062.836$ links. Finally, we simulated a Growing Network by using preferential attachment rule for 90% of new links [2] . The graph consists of $ 10.000$ nodes with constant out-degree $ d=8$.

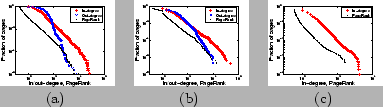
Cumulative log-log plots for in/(out)-degree and PageRank: (a) EU-2005, (b) Wikipedia, (c) Growing Network

Figure 1: Cumulative log-log plots for in/(out)-degree and PageRank: (a) EU-2005, (b)Wikipedia, (c) Growing Network

In Figure 1 we show the cumulative log-log plots for in-degrees, out-degrees and PageRank scores in all data sets. The PageRank scores in the network of $ n$ nodes are computed according to the classical definition [6]:
$\displaystyle PR(i) = c \sum_{j \to i} \frac{1}{d_{j}} PR(j) + \frac{c}{n} \sum_{j\in {\mathcal D}}PR(j)+\frac{1-c}{n}, \; i=1,\ldots,n,$

where $ PR(i)$ is the PageRank of page $ i$, $ d_j$ is the number of outgoing links of page $ j$, the sum is taken over all pages $ j$ that link to page $ i$, $ {\mathcal D}$ is a set of dangling nodes, and $ c$ is the damping factor, which is equal $ 0.85$ in our case. Throughout the paper we use the scaled PageRank scores $ R(i)=nPR(i).$

The log-log plots for in-degree and PageRank in Figure 1 resemble the signature straight line indicating power laws. However, several techniques should be combined in order to establish the presence of heavy tails and to evaluate the power law exponent. Using QQ plots, Hill and altHill plots as well as Pickands plots [7] we confirm that the in-degree and PageRank follow power laws with similar exponents for all three data sets. We also conclude that the out-degree can be modeled reasonably well as a power law with exponent around 2.5-3, see [8] for details.

Although all plots in Figure 1 look alike, it does not imply that the three networks have identical structure. The main goal of the present work is to rigorously examine the dependencies between the network parameters.


3 Angular Measure

Suppose we are interested in analyzing the dependencies between two regular varying characteristics of a node, $ X$ and $ Y$. Let $ X_j$ and $ Y_j$ be observations of $ X$ and $ Y$ for the corresponding node $ j$. Following [7], we start by using the rank transformation of (X,Y), leading to $ \{(r^{x}_{j},r^{y}_j),\;1 \leq j \leq n\},$ where $ r_j^{x}$ is the descending rank of $ X_j$ in $ (X_1,\ldots,X_n)$ and $ r_j^{y}$ is the descending rank of $ Y_j$ in $ (Y_1,\ldots,Y_n)$. Next we choose $ k=1,\dots,n$ and apply the polar coordinate transform as follows
POLAR$\displaystyle \left(\frac{k}{r_j^{x}},\frac{k}{r_j^{y}}\right)=(R_{j,k},\Theta_{j,k}),$ (1)

where POLAR$ (x,y)=\left(\sqrt{x^2+y^2},\arctan{(y/x)}\right)$.

Now we need to consider the points $ \{\Theta_{i,k}:R_{i,k}>1\}$ and make a plot for cumulative distribution function of $ \Theta$. In other words, we are interested in the angular measure, i.e. in the empirical distribution of $ \Theta$ for $ k$ largest values of $ R$. Thus, unlike the correlation coefficient, the angular measure provides a subtle characterization of the dependencies in the tails of X and Y, or, extremal dependencies. If such measure is concentrated around $ \pi/4$ then we observe a tendency toward complete dependence, when a large value of $ X$ appears simultaneously with a large value of $ Y$. In the opposite case, when such large values almost never appear together, we have either large value of $ X$ or large value of $ Y$, hence, $ \Theta$ should be around 0 or $ \pi/2.$ The middle case plots can be seen as a tendency to dependency or independency.

In the case of bi-variate data, a suitable value of $ k$ can be determined by making a Starica plot [7]. We consider radii $ R_{1,k},\ldots,R_{n,k}$ from (1) and write $ R_{(i)}$ for the $ i$th largest value. To get Starica plot we graph

$\displaystyle \left\{\left(R_{(j)}/R_{(k)},{jR_{(j)}}/kR_{(k)}\right),\;1\leq j\leq n\right\}.$

The idea is that for good $ k$ the ratio in the ordinate should be roughly a constant and equal 1 for the values of the abscissa in the neighborhood of 1. The plot looks different for the different parameters $ k$ and one can either find a suitable $ k$ by trial and error or use numerical algorithms. In general, if the plot is going steep up from $ y=1$ at $ x=1$ then the chosen $ k$ is too large. On the other hand, if the graph stabilizes around $ y=1$ for some $ x<1$ then it means that $ k$ is too small, and we miss some valuable tail data. In Figure 2(a) we show the Starica plot for in-degree and PageRank in the Web data sets for $ k=100.000$ as an example. We refer to [8] for more details and results.

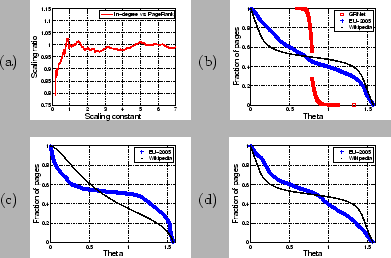
(a) Starica plot for in-degree and PageRank for EU-2005 data set; Cumulative functions for Angular Measures: (b) in-degree and PageRank;(c) in- and out-degrees; (d) out-degree and PageRank

Figure 2: (a) Starica plot for in-degree and PageRank for EU-2005 data set; Cumulative functions for Angular Measures: (b) in-degree and PageRank; (c) in- and out-degrees; (d) out-degree and PageRank

4 Dependence measurements

We computed the pairwise angular measure for the suitable $ k$'s determined in [8]. In Figure 2(b-d) we depict $ \theta\in[0,\pi/2]$ against the fraction of observations where the angle $ \Theta$ is greater or equal to $ \theta$.

The results are striking. For the Wikipedia data set we observe the independence of the tails of in-degree and PageRank. That is, an extremely high in-degree almost never implies an extremely high ranking. The picture is completely opposite for Growing Networks, where the angular measure is indicating a complete dependence. Thus, in highly centralized preferential attachment graphs, most connected nodes are also most highly ranked. Finally, the Web graph exhibits a subtle dependence structure with an angular measure close to uniform on $ [0,\pi/2]$. This suggests that the PageRank popularity measure can not be replaced by in-degree without significant disturbance in the ranking.

The picture is different in Figure 2(c). In the Web, the in- and out-degree tend to be independent which justifies the distinction between hubs and authorities. In Wikipedia the degrees are dependent but this dependence is not absolute. Finally, the dependence between out-degree and PageRank in the Web and Wikipedia resembles the patterns observed for in-degree and PageRank.

These results are useful in several ways. First, they reveal some important structural features thus extending our knowledge on real-life networks. Second, by comparing the dependencies for experimental and synthetic data we can considerably improve existing graph models.

REFERENCES

[1] http://law.dsi.unimi.it/ Accessed in January 2007

[2] R. Albert and A. L. Barab\'{a}si, Emergence of scaling in random networks, Science, 286:509-512, 1999

[3] D. Chakrabarti and C. Faloutsos, Graph mining: Laws, generators, and algorithms, ACM Comput. Surv., 38(1):2, 2006

[4] D. Donato, L. Laura, S. Leonardi, and S. Millozi, Large scale properties of the webgraph, Eur. Phys. J., 38:239-243, 2004

[5] S. Fortunato, M. Boguna, A. Flammini, and F.Menczer, How to make the top ten: Approximating PageRank from in-degree, In Proceeding of WAW2006, 2006

[6] A. N. Langville and C. D. Meyer, Deeper inside PageRank, Internet Math., 1:335-380, 2003

[7] S. I. Resnick, Heavy-tail Phenomena, Springer, New York, 2007

[8] Y.Volkovich, N. Litvak, and B. Zwart, Measuring extremal dependencies in web graphs, Memorandum 1858, http://eprints.eemcs.utwente.nl/11349/, 2007