Externalities in Online Advertising

Arpita Ghosh

Yahoo! Research
Santa Clara, CA

Mohammad Mahdian

Yahoo! Research
Santa Clara, CA

Copyright is held by the World Wide Web Conference Committee (IW3C2). Distribution of these papers is limited to classroom use, and personal use by others.
WWW 2008, April 21-25, 2008, Beijing, China.
ACM ???.

ABSTRACT

Most models for online advertising assume that an advertiser's value from winning an ad auction, which depends on the clickthrough rate or conversion rate of the advertisement, is independent of other advertisements served alongside it in the same session. This ignores an important externality effect: as the advertising audience has a limited attention span, a high-quality ad on a page can detract attention from other ads on the same page. That is, the utility to a winner in such an auction also depends on the set of other winners.

In this paper, we introduce the problem of modeling externalities in online advertising, and study the winner determination problem in these models. Our models are based on choice models on the audience side. We show that in the most general case, the winner determination problem is hard even to approximate. However, we give an approximation algorithm for this problem with an approximation factor that is logarithmic in the ratio of the maximum to the minimum bid. Furthermore, we show that there are some interesting special cases, such as the case where the audience preferences are single peaked, where the problem can be solved exactly in polynomial time. For all these algorithms, we prove that the winner determination algorithm can be combined with VCG-style payments to yield truthful mechanisms.

Categories & Subject Descriptors

F.2.0 Analysis of Algorithms and Problem Complexity [General]

J.4 Social and Behavioral Sciences [Economics]

General Terms

Algorithms, Economics, Theory

Keywords

Advertising, externalities, auctions, approximation algorithms

1 Introduction

Much of the work on auctions for online advertising assume that a bidder has an intrinsic value for winning an auction: given that a bidder is declared a winner of an ad slot, he derives some private utility, which is unaffected by the number or set of other winners. However, this is not necessarily true, especially in the context of advertising: advertisers compete for users' attention, and the attention a particular winning advertiser receives clearly depends on the set of all winners. In this paper, we are interested in the problem of mechanism design in a setting with externalities, i.e., when a winner's utility depends on the set of other winners.

The problem of mechanism design with externalities can be motivated in multiple settings in the context of online advertising, for instance, in the setting of sponsored search (e.g., Google's Adwords or Yahoo!'s Search Marketing) or ad placement on content pages (e.g., Google's Adsense or Yahoo!'s Content Match). In this paper we focus on a setting commonly known as online lead generation, or the pay-per-lead model [11]. The objective of online lead generation is to sell credible leads (in the form of personal information of a potential customer) to companies, or advertisers, interested in such leads. The advertisers then contact the potential customer directly to offer quotes and information about their service. This model of advertising is currently most popular among financial firms that offer mortgages, insurance companies, auto dealers interested in potential buyers of new cars, and the distance education industry1. According to the PricewaterhouseCoopers' IAB Revenue Report for year 2006 [12], lead generation revenues accounted for 8 percent of the 2006 full year revenues or $1.3 billion, up from the 6 percent or $753 million reported in 2005. In addition to having been the initial motivation of the present work, focusing on the lead generation model has the advantage that it simplifies the discussion of externalities by abstracting away aspects of the problem relating to the specific placement of the ads on a page. We will briefly discuss such issues and their interplay with the externality problem at the end of this paper.

The main problem faced by a lead generation company that has acquired a lead is the following tradeoff: if the lead is sent to fewer advertisers, the value to each advertiser will be higher since they are competing with fewer other advertisers for the potential customer. Further, the value to an advertiser might also depend specifically on which other advertisers obtain the lead, not just how many others: a competing advertiser who provides a similar service and is very likely to offer a better deal to the user decreases the value of the lead much more than a less competitive advertiser, or an advertiser who is offering a different service (e.g., a Toyota dealer might decrease the value to a Honda dealer more than a Ford dealer does). In any case, the utility to an advertiser who buys a lead depends on other buyers of the same lead. In addition, typically a lead can only be sold to a limited number of advertisers, as specified in the privacy policy of the website [11].

In the most general and abstract form, the problem we are interested in is the following: there are $ n$ bidders, each with a utility function $ u_i: 2^{\{1,\ldots,n\}}\mapsto\mathbf{R}$, where $ u_i(S)$ is the utility that bidder $ i$ derives when the set of winners is $ S\subset \{1, \ldots, n\}$. It is reasonable to assume that $ u_i(S)$ is zero if $ i \notin S$. The problem is to design an incentive compatible mechanism to maximize welfare. Such a mechanism would select the subset of bidders that maximizes

$\displaystyle v(S) = \sum_{i \in S} u_i(S). $
VCG payments can be used to induce truthful reporting if the optimal subset can be found: every bidder $ i$ is charged the difference between the value of the optimal set when $ i$ is removed from the set of bidders and $ v(S) - u_i(S)$, which is the value derived by all remaining winners in the current solution.

Since specifying a utility function of the form above takes exponential space in the number of bidders, we are interested in investigating models for utility functions that are both realistic in the context of online advertising, and also allow compact representation. We build such a model by looking at the choice problem from the advertising audience's perspective. Our model assumes that customers have (possibly interdependent) valuations for different advertisers (these valuations might be a function of the quote the customer receives from the advertisers in a lead generation business, or the perception of the quality of the product offered by the advertiser) and also for an outside option. When presented with a number of choices, they pick the advertiser whom they have the highest valuation for, or no advertiser if their valuation of the outside option is greater than the valuations of all advertisers presented in the set. This model is defined in more detail in the next section. We will study the computational complexity of the winner determination problem in this model, and prove that in the most general case, if the distributions of the values are given explicitly, the winner determination problem is hard to approximate within a constant factor. On the other hand, we will give an approximation algorithm that solves this problem within a factor that is logarithmic in the ratio of the maximum to the minimum bid. Furthermore, in several special cases, most notably in the case that distributions are single-peaked, the winner determination problem can be solved exactly in polynomial time. We will prove that these algorithms, combined with a VCG-style payment scheme, give rise to dominant-strategy incentive compatible mechanisms.

Finally, we discuss alternative models for externalities, and directions for future work.


Related work. Auctions with externalities have been studied in the economics literature, the earliest related work being that of Jehiel, Moldovanu and Stacchetti [7], where a loser's value depends on the identity of the winner. The problem of mechanism design with allocative externalities is also studied by Jehiel and Moldovanu [5], and Jehiel, Moldovanu and Stacchetti [8]; [6] studies mechanism design with both allocative and informational externalities. However, none of these papers address computational issues arising from the mechanism design problem.

To the best of our knowledge, this is the first theoretical work that specifically addresses the problem of externalities in online advertising. Limited experimental evidence for the hypothesis that the click-through rate of ads depend on surrounding ads is provided in the work of Joachims et al. [9].

2 The model

In this section, we define a model for externalities among advertisers that is the focus of this paper. Our model is based on the intuition that each advertiser has a private value for capturing the business of the user (the advertising audience). The user, on the other hand, gets exposed to a number of ads, and chooses at most one of these ads based on her perception of the quality of the advertiser. For example, in the case of the lead generation business, the user receives quotes from the advertisers who receive the lead, and probably will choose the advertiser who gives her the lowest quote, or none of the advertisers, if she receives a better quote through another medium.

More formally, suppose there are $ n$ advertisers numbered $ 1, \ldots, n$, each with a private value $ v_i$ (which is the value advertiser $ i$ derives when he is chosen by a user). The quality of advertiser $ i$ (from the perspective of the user) is denoted by $ q_i$. Furthermore, let $ q_0$ denote the quality of the best outside option. These quality parameters $ q_i$ are random variables, drawn from a joint probability distribution $ {\cal Q}$. Intuitively, considering $ q_i$'s as random variables (as opposed to deterministic values) captures the fact that users do not all make the same choices among the advertisers. Also, in general the $ q_i$'s need not be independent, since the choices of users are often dictated by the same general principles. For example, knowing that a user perceives Ford autos as superior to Toyotas increases the likelihood that she also prefers Chevy to Honda.

When a set $ S$ of advertisers is chosen, the user picks the advertiser with the largest quality $ q_i$ in $ S$, if the quality of this advertiser is greater than that of the outside option. This advertiser then derives a value of $ v_i$; all other advertisers derive a value of 0. So the expected value when a set $ S$ of advertisers is chosen is

$\displaystyle v(S) = \sum_{i \in S} v_i {\mathrm{Pr}}[\forall j \in S \cup \{0\}:~ q_i \geq q_j], $
where the probability is over a random draw of $ (q_0,q_1,\ldots,q_n)$ from $ {\cal Q}$. For simplicity, we assume that $ q_i$'s are always distinct, and therefore we do not need to specify how ties are broken.

The winner determination problem in this model is to choose a set $ S$ of at most a given number $ k$ of advertisers to maximize $ v(S)$. Note that $ v(S)$ is not monotone in $ S$: adding an advertiser with low value but high quality can actually cause a net decrease in the value of the set. The winner determination problem can be written as the following mathematical program:

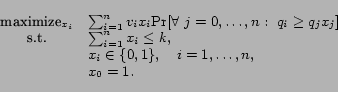\begin{displaymath}\begin{array}{cl} \mbox{maximize}_{x_i} &\sum_{i=1}^n v_i x_i... ... \in \{0,1\}, \quad i = 1, \ldots, n, \\ & x_0 = 1. \end{array}\end{displaymath} (1)

Before we can start talking about the computational complexity of the winner determination problem, we need to specify how the input is represented. In particular, there are many ways the distribution $ {\cal Q}$ can be represented. In this paper, we mainly consider an explicit representation of $ {\cal Q}$, i.e., when the distribution has a finite support and all elements of the support of this distribution are listed as part of the input (as explained below). This is perhaps the simplest way to represent the distribution, and our hardness result in the next section (showing that the winner determination problem is hard to approximate for this representation) clearly carries over to stronger representations, such as models where $ {\cal Q}$ is given by an oracle.

Observe that in our model, the actual values of the quality parameters $ q_i$ do not matter; all that matters is the relative ordering of the qualities. Specifically, the only real information we use from the distribution is the probability of each ranking of the bidders' qualities and the quality of the outside option. In other words, we can assume that there are a finite number of different user types, and each user type $ j$ is given by a real number which indicates the probability that a random user is of type $ j$, and a permutation of the $ n+1$ options $ \{0,\ldots,n\}$ (with 0 representing the outside option and $ 1, \ldots, n$ representing the advertisers). Note that the ordering of advertisers that occur after the outside option in a permutation is irrelevant, and therefore can be omitted. To summarize, the externality problem with an explicitly given distribution can be formulated as follows.



WINNER DETERMINATION PROBLEM WITH EXTERNALITIES:
INPUT:
-
Integers $ n$, $ m$, and $ k$,
-
a value $ v_i$ for each $ i=1,\ldots,n$,
-
a probability $ p_j$ for each $ j=1,\ldots,m$
with $ \sum_{j=1}^m p_j=1$, and
-
a permutation $ \pi_j$ of $ \{0,\ldots,n\}$
for each $ j=1,\ldots,m$.

OUTPUT: A subset $ S$ of $ \{1,\ldots,n\}$ with $ \vert S\vert\le k$ that maximizes
$\displaystyle v(S):=\sum_{j=1}^m p_j\sum_{i\in S} v_i I(\forall\ l\in S\cup\{0\}:\ \pi_j(i)\le\pi_j(l)), $
where $ I(\forall\ l\in S\cup\{0\}:\ \pi_j(i)\le\pi_j(l))$ denotes the indicator variable for the event that $ i$ is the highest element in permutation $ \pi_j$ of all members of $ S\cup 0$.


In the next section, we will show a strong hardness result for the above problem. In Section 4 we will give an approximation algorithm, and in Section 5 we prove that the problem is solvable in polynomial time if preferences $ \pi_j$ are single-peaked, and also in another special case of the problem with implicitly given distributions.


3 Hardness of the winner determination problem

We show that the winner determination problem defined in the previous section, even with no cardinality constraints (i.e., $ k=n$), is NP-hard, and hard to approximate. The proof is based on a reduction from the independent set problem in graphs. Recall that in the independent set problem, we are given a graph $ G$ and the objective is to find a maximum-cardinality subset $ S$ of vertices with no edge between any two vertices of $ S$. Håstad [14] proved that this problem cannot be approximated in polynomial time to within a factor of $ n^{1-\epsilon}$ for any $ \epsilon > 0$, unless $ {\bf NP}= {\bf ZPP}$.
Theorem 1 The winner determination problem with externalities is hard to approximate in polynomial time within a factor $ n^{1-\epsilon}$ for any $ \epsilon > 0$, unless $ {\bf NP}= {\bf ZPP}$.
Proof. Given an instance $ G$ of the independent set problem, we map it to an instance of the winner determination problem with externalities as follows. Let $ n=m=k=\vert V(G)\vert$, and assume the nodes in the graph $ G$ are numbered $ 1, \ldots, n$. Corresponding to each node $ i$, we create an advertiser $ i$ with value $ v_i = L^i$, where $ L$ is a sufficiently large number (as we will see, it is enough to take $ L=n^2$). Also, for each node $ i$, we create a user type $ i$ with probability $ p_i=c/L^i$, where $ c$ is a normalizing constant that ensures $ \sum_{i=1}^n p_i=1$.

The permutation $ \pi_i$ corresponding to user type $ i$ is constructed as follows. Let $ N^-_i:=\{j: j<i$ and $ ij\in E(G)\}$ denote the set of neighbors of $ i$ in $ G$ that have an index less than $ i$. The permutation $ \pi_i$ ranks the elements of $ N^-_i$ in an arbitrary order at the top, followed by $ i$, followed by the outside option 0 (recall that the ordering of elements after the outside option is not important). This completes the definition of the instance of the winner determination problem.

Now, we show that if the size of the maximum independent set in the graph $ G$ is $ t$, then the value of the solution of the above instance of the winner determination problem is between $ ct$ and $ ct+\frac{cn}{L}$.

Let $ I$ denote the maximum independent set of $ G$ ($ \vert I\vert=t$). First, we prove that the value of the solution to the winner determination problem is at least $ ct$. To show this, it is enough to take $ S=I$. Since $ I$ is an independent set, for every $ i\in S$, the first element of $ \pi_i$ that is in $ S$ is $ i$. Therefore, for every such $ i$, users of type $ i$ contribute a total value of $ p_i\times v_i = c$ to the objective function. Hence, the value of the set $ S$ is precisely $ v(S)=ct$.

Next, we prove that no set $ S$ in the instance of the winner determination problem has value more than $ ct+\frac{cn}{L}$. To show this, take the optimal set $ S$ in the winner determination problem, and define an independent set $ I$ in the graph as follows: start with $ I=\emptyset$, and process vertices of $ S$ in increasing order of their index. For every vertex $ i\in S$, if no neighbor of $ i$ is added to $ I$ so far, add $ i$ to $ I$. Clearly, at the end of this procedure, we obtain an independent set $ I$ of $ G$. We show that the value of the set $ S$ is at most $ c\vert I\vert+\frac{cn}{L}$. To see this, note that for every element $ i$ that is in $ S$ but not in $ I$, the vertex $ i$ must have a neighbor $ j\in S$ with $ j<i$. Consider such a $ j$ with the smallest index. By definition, $ j$ appears before $ i$ in $ \pi_i$. Therefore, the contribution of each such user type $ i$ to $ v(S)$ is at most $ p_iv_j\le c/L$. For every $ i\in I$, the contribution of $ i$ to $ v(S)$ is at most $ p_i v_i=c$. Summing up these contributions, we obtain $ v(S)\le c\vert I\vert + \frac{cn}{L}$. Since $ I$ is an independent set, we get $ v(S)\le ct+\frac{cn}{L}$.

Therefore, if we take $ L>n^2$, the value of the solution of the winner determination problem divided by $ c$ is within $ (1\pm o(1))$ of the size the maximum independent set of $ G$. Thus, by the hardness of the independent set problem [14], the winner determination problem cannot be approximated within a factor of $ n^{1-\epsilon}$ for any $ \epsilon > 0$, unless $ {\bf NP}= {\bf ZPP}$. $ \qedsymbol$

The above theorem rules out the possibility of finding an algorithm for the winner determination problem with any approximation factor that is a reasonable function of $ n$. However, note that the instances constructed in the above hardness result contain advertisers whose values differ by a large factor ($ n^{2n}$). This raises the question of whether one can approximate the winner determination problem within a factor that depends on the spread between the largest and the smallest values. The answer to this question is indeed positive, as we will see in the next section.


4 Approximation algorithm

We now present an approximation algorithm for the winner determination problem which can be used to design an incentive compatible mechanism for the auction problem with externalities. The hardness result in the previous section rules out any approximation that is better than a linear factor in the number of advertisers; our approximation is therefore in terms of the spread of the advertiser values: we show that the winner determination problem can be approximated to within a factor of $ \frac{e^2}{e-1}(\lceil \ln R \rceil + 1)$, where $ R$ is an upper bound on the ratio between the highest value and the lowest value an advertiser could have.

We begin with the following lemma, which shows that the problem can be solved approximately when all values are close to each other.

Lemma 1 The winner determination problem can be approximated to within a factor $ \frac{e}{e-1}R$, where $ R$ is an upper bound on the ratio between the highest value and the lowest value an advertiser could have.
Proof. First suppose that $ v_1 = \ldots = v_n$, i.e., all advertiser values are equal. Then the problem of winner determination with externalities is exactly a weighted version of the classical max $ k$-coverage problem [15]: the elements are the $ m$ user types with weights $ p_j$ ( $ j=1,\ldots,m$), the sets are the advertisers $ i=1,\ldots,n$, and an advertiser $ i$ covers a user type $ j$ if $ i$ appears in $ \pi_j$ before 0, i.e., if user type $ j$ prefers $ i$ over the outside option.

The greedy approximation algorithm for the maximum $ k$-coverage problem can be easily generalized to solve the weighted version: the algorithm proceeds in iterations, in each iteration picking an advertiser that covers a set of previously uncovered user types of maximum total weight. It is not hard to see that this algorithm achieves an approximation factor of $ e/(e-1)$ for the weighted maximum $ k$-coverage problem [15]. The winner determination problem can be approximated to within the same factor when all values are equal. If advertisers have unequal values, we can obtain a factor $ \frac{e}{e-1}R$ by simply ignoring the values and solving the weighted max-coverage problem. $ \qedsymbol$

We will now build on this observation to obtain a randomized algorithm with a ratio that is logarithmic in $ R$. Then we will show how this algorithm can be turned into a monotone algorithm (a property that is needed in order to achieve incentive compatibility), and how it can be derandomized.

For a given subset $ S \subseteq \{1, \ldots, n\}$, denote by $ OPT_k(S)$ the value of the optimal solution to the weighted max-$ k$-coverage problem restricted to the subset of advertisers $ S$, $ P_k(S)$ the value of the solution returned by the greedy algorithm to the weighted max $ k$-coverage problem, and denote by $ S^*_k(S)$ the subset of advertisers from $ S$ chosen by the greedy algorithm.

Assume $ v_{\min}$ is a known lower bound, and $ v_{\min}R$ is a known upper bound on the value of an advertiser. We will show later that our derandomized algorithm works even if we do not know the values of $ v_{\min}$ and $ R$. Divide advertisers into buckets $ 1$ through $ L$, where $ L=\lceil\ln R\rceil$ and bucket $ B_l$ consists of advertisers with values $ v_i \in [e^{l-1} v_{\min}, e^lv_{\min})$.



Algorithm $ A_1$:

Theorem 2 Algorithm $ A_1$ approximates the winner determination problem to within a factor of $ \frac{e^2}{e-1}\lceil\ln R\rceil$.
Proof. Let $ SOL_1$ denote the expected welfare from the solution chosen by the above algorithm:
$\displaystyle SOL_1 \geq \sum_{l=1}^{L} \frac{1}{L}v_{\min} e^{l-1} P_k(B_l),$ (2)

where $ P_k(B_l)$ is the weight of the solution chosen by the greedy algorithm for max $ k$-coverage, with input restricted to the set of advertisers with values in $ [e^{l-1} v_{\min}, e^{l} v_{\min}]$, as defined before.

The welfare from the optimal set of advertisers for the winner determination problem $ S_{OPT}$ is

$\displaystyle OPT$ $\displaystyle =$ $\displaystyle \sum_{i \in S_{OPT}} v_i P(i, S_{OPT})$
$\displaystyle =$ $\displaystyle \sum_{l = 1}^{L} \sum_{i \in S_{OPT} \cap B_l} v_iP(i, S_{OPT})$
$\displaystyle \leq$ $\displaystyle \sum_{l = 1}^{L} v_{\min} e^{l} \sum_{i \in S_{OPT} \cap B_l} P(i, S_{OPT}),$ (3)

where $ P(i,S_{OPT}) = \sum_{\{j: \forall i'\in S_{OPT}\cup\{0\},~\pi_j(i) \leq \pi_j(i')\}} p_j$ is the total weight of the permutations where $ i$ is ranked above all other elements in $ S_{OPT}$ and the outside option.

Since $ P_k(B_l)$ is the solution returned by the greedy algorithm for the maximum $ k$-coverage problem restricted to advertisers in $ B_l$, and $ S_{OPT}\cap B_l$ is a solution for this problem of value at least $ \sum_{i \in S_{OPT} \cap B_l}P(i,S_{OPT})$, we have

$\displaystyle \sum_{i \in S_{OPT} \cap B_l} P(i, S_{OPT}) \leq \frac{e}{e-1}P_k(B_l). $
Combining (2) and (3) with this, we get
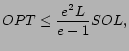
$\displaystyle OPT \leq \frac{e^2L}{e-1} SOL, $
i.e., an approximation factor of $ \frac{e^2}{e-1}\lceil\ln R\rceil$. $ \qedsymbol$

It is a well-known theorem (see, for example, Archer and Tardos [1]) that in a setting with one-dimensional types, in order to design an incentive compatible mechanism, one needs an allocation algorithm that is monotone: the probability of winning should not decrease if an advertiser's value increases. The above algorithm does not have this property: for example, if advertiser $ i$ is the only advertiser in an interval $ B_l$, she wins with probability $ 1/L$ independent of her position in the permutations, whereas she may not be chosen as a winner in her new bucket if her value increases.

The following modification ensures that the allocation algorithm is monotone.

Define the (overlapping) buckets

$\displaystyle \overline B_l = \{i: v_i \ge v_{\min}e^{l-1}\}, $
i.e., $ \overline B_l = B_l \cup \ldots \cup B_L$ is the union of the buckets $ B_j$ from $ l$ to $ L$. Denote by $ P_k(\overline B_l)$ the value of the greedy solution of the weighted max $ k$-coverage problem restricted to advertisers in $ \overline B_l$.



Algorithm $ A_2$:

Theorem 3 The algorithm $ A_2$ is monotone, and approximates the winner determination problem to within a factor of $ \frac{e^2}{e-1}\lceil\ln R\rceil$.
Proof. The proof of the approximation ratio follows simply from Theorem 2 and noting that
$\displaystyle P_k(\overline B_l) \geq P_k (B_l), $
since $ B_l \subseteq \overline B_l$. To prove the monotonicity, note that for any bucket $ \overline B_l$ and any advertiser $ i$, if this advertiser is in $ \overline B_l$, after increasing the value $ v_i$, she still remains in this bucket. Therefore, conditioned on any value of $ l$, increasing $ v_i$ (while holding everything else constant) cannot remove $ i$ from $ \overline B_l$ and therefore cannot decrease $ i$'s chance for being included in the solution. $ \qedsymbol$

Finally, we show that our algorithm can be derandomized while maintaining the monotonicity property. The idea of derandomization is easy: instead of picking a random bucket, check all buckets and pick one that gives the highest value. However, one needs to be careful as this transformation can sometimes turn a monotone algorithm into a non-monotone one. In our case, we can use properties of the greedy maximum $ k$-coverage algorithm to prove that the algorithm remains monotone.

In addition to decreasing uncertainty, one advantage of the derandomized algorithm is that it can be implemented without knowledge of the values of $ v_{\min}$ or even $ R$.2 In order to do this, for every integer $ l$, we define the bucket $ \overline B_l$ as the set of advertisers of value at least $ e^l$ ( $ \overline B_l = \{i: v_i\ge e^l\}$). By the definition of $ R$, there are at most $ \lceil\ln R\rceil+1$ non-empty distinct buckets. We can now define the deterministic algorithm as follows:



Algorithm $ A_3$:

Theorem 4 The algorithm $ A_3$ is monotone, and approximates the winner determination problem to within a factor of $ \frac{e^2}{e-1}(\lceil \ln R \rceil + 1)$, where $ R$ is an upper bound on the ratio between the highest value and the lowest value an advertiser could have.
Proof. The approximation ratio follows from Theorem 3 and the fact that the maximum of a set of numbers is not less than their average. We now prove that the algorithm $ A_3$ is montone. Suppose that bidder $ i$ is a winner, and has value $ v_i \in [e^{l}, e^{l+1})$, i.e., $ i$ is in bucket $ \overline B_l$ and every bucket before that. Since she is a winner, $ e^j P_k(\overline B_j)$ is maximized for some $ j=l^* \leq l$. Suppose $ v^+_i > v_i$ is such that $ v^+_i \in [e^{l^+},e^{l^++1})$. We need to show that after increasing $ i$'s value to $ v^+_i$, $ i$ is still a winner.

Note that $ P(\overline B_{l'})$ is unchanged for all $ l' \leq l$, since $ \overline B_{l'}$ is unchanged for these sets, and the values of bidders in $ \overline B_{l'}$ do not affect the value of $ P(\overline B_{l'})$, or the set of bidders corresponding to $ P(\overline B_{l'})$. For the sets $ \overline B_{l'}$ with $ l < l' \leq l^+$, the only addition is the bidder $ i$. Since the algorithm used to compute $ P(\overline B_{l'})$ is the deterministic greedy algorithm for weighted max-$ k$ coverage [15], $ P(\overline B_{l'})$ changes only if the algorithm chooses $ i$ in the winning set. Thus if $ P(\overline B_{l'}) \geq P(\overline B_{l^*})$, $ i$ is chosen as a winner in $ \overline B_{l'}$. Therefore, the allocation algorithm is monotone. $ \qedsymbol$

The above theorem, together with the theorem of Archer and Tardos [1] implies that there is a dominant-strategy incentive-compatible mechanism for ad auctions with externalities that can approximate the social welfare to within a factor of $ \frac{e^2}{e-1}(\lceil \ln R \rceil + 1)$ of the optimum.


5 Algorithms for special classes of user preferences

The result in the previous section says that the problem of choosing the optimal set of advertisers cannot even be approximated well, in the most general case. However, as we will show in this section, the problem can be solved exactly in certain special cases.

1 Single-peaked preferences

Single-peaked preferences form an important domain of preferences, and are well-studied in the contexts of majority voting and Arrovian social welfare functions, strategyproof voting rules, and fair division, among others (see, for example, [3,13]).

We start by defining the notion of single-peaked preferences in the context of the externality problem. Recall that the preference of each user type $ j$ is given as a permutation $ \pi_j$ of $ \{0,1,\ldots,n\}$, where 0 is the outside option and $ 1, \ldots, n$ represent advertisers. We say that the user preferences are single-peaked (with respect to the ordering $ 1, \ldots, n$ of the advertisers), if for every user type $ j$, there is a value $ a_j\in\{1,\ldots,n\}$, such that for every $ 1\le x<y\le a_j$, advertiser $ y$ is preferred to advertiser $ x$ according to $ \pi_j$, and for every $ a_j\le x<y\le n$, advertiser $ x$ is preferred to advertiser $ y$ according to $ \pi_j$. In other words, each user type $ j$ has an ideal advertiser $ a_j$, and advertisers before $ a_j$ are ranked according to their distance to $ a_j$, and similarly for advertisers after $ a_j$. No restriction is placed on how $ j$ ranks two advertisers, one before $ a_j$ and the other after $ a_j$, or how she ranks any advertiser in comparison to the outside option.

The following theorem gives an algorithm for the winner determination problem with externalities, when preferences are single-peaked, with respect to a known ordering $ 1, \ldots, n$.

Theorem 5 The winner determination problem with externalities can be solved in polynomial time if user preferences are single-peaked.
Proof. We give a dynamic programming algorithm for this problem. The main step is to define an appropriate subproblem, which can be solved recursively. The subproblem we use is parameterized by two parameters $ i$ and $ r$, with $ 1\le i\le n$ and $ 1\le r\le k$, and is defined as follows:
Consider an instance of the winner determination problem with externalities where the set of user types is restricted to $ \{j: a_j\ge i\}$ (note that we do not change the probabilities $ p_j$'s, so in this restriction the probabilities can add up to less than 1. However, the problem is still well-defined in this case). Let $ SOL_{i,r}$ be the maximum value $ v(S)$ of a set $ S$ satisfying the following: $ i\in S$, $ S\subseteq\{i,\ldots,n\}$, and $ \vert S\vert\le r$.

We show how $ SOL_{i,r}$ can be computed recursively. The idea is to focus on the first advertiser after $ i$ that will be included in the set $ S$. If $ i'$ is the index of this advertiser, the value derived from user types $ j$ with $ a_j\ge i'$ can be written as $ SOL_{i',r-1}$, since by the single-peaked property of the preferences, none of these users prefers any advertiser before $ i'$ to $ i'$. Users $ j$ with $ i\le a_j< i'$ will choose one of the advertisers $ i$ and $ i'$ or the outside option (again, by the single-peaked property). Therefore, the total value of the solution in this case can be written as

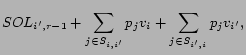
$\displaystyle SOL_{i',r-1} + \sum_{j\in S_{i,i'}} p_jv_i + \sum_{j\in S_{i',i}} p_jv_{i'}, $
where $ S_{i,i'}:=\{j:~ \min(i,i')\le a_j<\max(i,i')$ and $ \pi_j(i)<\min(\pi_j(i'),\pi_j(0))\}$ is the set of users whose ideal advertiser is between $ i$ and $ i'$ and prefer $ i$ to $ i'$ and also to the outside option. To compute $ SOL_{i,r}$, we need to take the maximum over all $ i'$ of the above expression, and also of the case where there is no such $ i'$, i.e., $ i$ is the last advertiser that is included in the set. In this case, the value of the subproblem is $ \sum_{j\in S_{i,n+1}}p_jv_i$, where $ S_{i,n+1}:=\{j: a_j\ge i$ and $ \pi_j(i)<\pi_j(0)\}$ is the set of users whose ideal advertiser is after $ i$ and who prefer $ i$ to the outside option. To summarize, $ SOL_{i,r}$ can be computed using the following recursive formula for every $ r\ge 2$.
$\displaystyle SOL_{i,r}$ $\displaystyle =$ $\displaystyle \max\{\sum_{j\in S_{i,n+1}}p_jv_i, \max_{i'>i}\{SOL_{i',r-1}$ (4)
$\displaystyle + \sum_{j\in S_{i,i'}} p_jv_i + \sum_{j\in S_{i',i}} p_jv_{i'}\}\}.$ (5)

For $ r=1$, we have $ SOL_{i,r}=\sum_{j\in S_{i,n+1}}p_jv_i$. Using the above recursions, one can compute all the $ SOL_{i,r}$'s in time $ O(n^2km)$. Using the above argument, it is easy to see that the solution of the problem can be computed in terms of these values as follows:

$\displaystyle \max_{i=1,\ldots,n}\left\{\sum_{j\in S_{0,i}} p_jv_i + SOL_{i,r}\right\},$
where $ S_{0,i}=\{j:~ a_j<i$ and $ \pi_j(i)<\pi_j(0)\}$ is the set of users whose ideal advertiser is before $ i$ and who prefer $ i$ to the outside option. This gives an $ O(n^2km)$-time algorithm to solve the winner determination problem with externalities when user preferences are single-peaked. $ \qedsymbol$
Remark 1 Note that the size of the dynamic programming table in the above algorithm is $ O(nk)$, which is independent of the number of different user types. Therefore, our algorithm can be adapted to the cases where there are exponentially many user types, and they are given either by an oracle, or with an implicit representation. The only ingredient needed is an algorithm that computes summations like the ones in Equation (4).

2 Perturbed single ranking

We now consider another special case of the winner determination problem, where user preferences are given implicitly using the following distribution of advertiser qualities: Advertiser $ i$ has quality $ q_i = x_i$ with probability $ p_i$ (where $ x_i$'s are a given distinct values), and $ -1$ with probability $ 1-p_i$; the quality is independent of all other advertisers' qualities. The quality parameter for the outside option is fixed at $ q_0=0$. This gives rise to exponentially many permutations which are all subsets of a single underlying permutation defined by the $ x_i$'s, but each advertiser $ i$ is dropped from the permutation (independently) with probability $ 1-p_i$.

An interpretation of this model is that there is an underlying true quality rating amongst all advertisers (as given by the ordering of the $ x_i$'s), and a user who is informed about two advertisers $ i$ and $ j$ ranks them in this order. However, with probability $ 1-p_i$, the user has not heard of advertiser $ i$, in which case she will not choose this advertiser. In other words, users rank the advertisers according to independent perturbations of the same ranking, under a particular model of perturbation. As we will point out in Remark 2, the idea can be generalized to more general ``local'' perturbation models.

The value of a set of advertisers $ S$ in this model can be written as

$\displaystyle v(S) = \sum_{i \in S} v_ip_i \prod_{j \in S, x_j>x_i} (1-p_j).$ (6)

Theorem 6 The winner determination problem in the above model can be solved exactly in polynomial time.
Proof. Again, we use dynamic programming to give a $ \Theta(nk)$-time algorithm for the winner determination problem.

Number advertisers in decreasing order of $ x_i$, so that $ x_1 > x_2 > \cdots > x_n$. We consider the following subproblem: Let $ SOL_{i,r}$ denote the optimal value when no more than $ r$ advertisers can be selected from the subset $ i, \ldots, n$ of advertisers. In other words, $ SOL_{i,r}:=\max_{S\subseteq\{i,\ldots,n\}, \vert S\vert\le r}\{v(S)\}$.

Note that $ v(S \cup \{i\})$ for $ i < \min(S)$ is $ p_iv_i + (1-p_i)v(S)$. Using this, it is easy to prove the following recursion.

$\displaystyle SOL_{i,r} = \max(SOL_{i+1,r}, v_ip_i + (1-p_i)SOL_{i+1,r-1}). $
Starting from $ i = n$ ( $ SOL_{n,r} = p_nv_n$ for all $ r$), we populate a table with $ nk$ entries; computing each entry in the table takes $ \Theta(1)$ time. Therefore, the solution of the winner determination problem, which is given by $ SOL_{1,k}$, can be computed in time $ O(nk)$. $ \qedsymbol$
Remark 2 Note that the only thing our algorithm relies on is that if $ i$ is before all elements of $ S$, $ v(S \cup \{i\})$ can be computed from $ v(S)$. For many other models of perturbation that perturb the permutation locally and independently, a similar approach works, perhaps by keeping a limited amount of information about the set $ S$. As an example, consider perturbations of the following form: swap the order of the advertisers $ 2i-1$ and $ 2i$ in the underlying permutation with probability $ p'_i$, independently for all $ i$; then from the resulting permutation, drop element $ j$ with probability $ p_j$, independently for all $ j$. If $ i$ is before all elements of $ S$, $ v(S \cup \{i\})$ can be computed given $ v(S)$ and the lowest-index element of $ S$. Therefore, the winner determination problem can be solved in this perturbation model by a dynamic programming algorithm with an $ n\times n\times k$ table.

6 Alternative models

In this section we discuss two other models that are not based on a model of users' choices, but are simpler and therefore might be more applicable in practice.


Pairwise multiplicative model. As before, there are $ n$ advertisers with private values $ v_1, \ldots, v_n$. The model is defined in terms of parameters $ a_{ij}\in[0,1]$ for $ 1\le i,j\le n$. The value of $ a_{ij}$ represents the factor by which advertiser $ j$ decreases the value to advertiser $ i$, if both are chosen together in the winning set. The value of a set $ S$ is

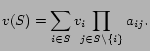
$\displaystyle v(S) = \sum_{i \in S} v_i \hspace{-2mm}\prod_{j \in S\setminus\{i\}}a_{ij}. $
In terms of the computational complexity of the winner determination problem, this problem is still hard to approximate, since by taking $ a_{ij}\in\{0,1\}$, one can see easily that the independent set problem is a special case of this problem.


Uniform discount model. This model assumes that different advertisers experience the same degree of discount, which depends only on total weight of the set of winners. More precisely, we assume each advertiser $ i$ has a private value $ v_i$ and a weight $ w_i$ (the weight could correspond to the conversion rate or another measure of the importance of the advertiser), and we are given a non-increasing function $ f:\mathbb{R}\mapsto[0,1]$, which specifies the discount as a function of the total weight of the advertisers in the set. The value of a set $ S$ is given by

$\displaystyle v(S) = \sum_{i \in S} v_i f(\sum_{j\in S}w_j). $
It is not hard to see that the winner determination problem in this model can be solved using the algorithm for the knapsack problem: for every level $ W$ of the total weight, we can compute the set $ S_W$ of advertisers of maximum total value whose weight add up to at most $ W$. This can be computed using a knapsack algorithm. The solution of the winner determination problem is the maximum, over all choices of $ W$, of the value of $ S_W$. With an appropriate discretization of values of $ W$, this can be made into a polynomial time approximation scheme for the problem. When weights are small integers, this approach gives a polynomial time exact algorithm for the problem. Turning the approximation scheme for the winner determination problem into a truthful mechanism remains an open question. One approach to tackle this problem would be to use the techniques developed in the context of multi-unit auctions [10].

7 Discussion

In this paper, we discussed models for the externality problem in online advertising. We proved that for the most general model, the winner determination problem is computationally hard, and gave algorithms for this problem in some special cases.

We believe that the externality problem is a major issue in the study of online advertising, and so far has not received enough attention from the research community. In the following, we list a few directions for future research.


Location-dependent externalities. The models studied in this paper, motivated by the lead generation business, was developed for a setting where the only decision made by the winner determination algorithm is the set of advertisers who get an advertising opportunity (by receiving a lead), without any particular order. However, in the cases where the auction decides which advertisements should be displayed on a page (which is the more common case), the winner determination algorithm should not only specify which ads are displayed, but also in which slot each ad is displayed. Furthermore, in this setting the externalities can be location dependent: for example, a sponsored search ad displayed in the 10th slot might impose no externality on the ad displayed on the top slot. Therefore, in order to be applicable to this setting, our model for externalities has to be modified to take the locations into account.

A simple way to incorporate the location component into our model is as follows: assume the slots are numbered $ 1,2,\ldots,K$, from top to bottom. We assume a random user only looks at the ads in the top $ X$ slots, where $ X$ is a random variable with a given distribution. The user then decides which of the ads she has looked at to click on, according to one of our models.

Clearly, our hardness result for the winner determination problem works for this more general model as well. It would be interesting to find interesting special cases of this problem that can be solved in polynomial time.


The long-term externality effect. In this paper, our focus was on the immediate externality that advertisers impose on each other, in terms of lowering the conversion rate or the click-through rate of other advertisers in the same session. There is also a long-term externality effect: if a user finds the ads displayed on a website (e.g., sponsored search ads on Google) helpful, he or she is more likely to click on ads in the future, and conversely, if the ads are found to be not relevant, the user will pay less attention to ads in the future. This externality effect is well understood in the context of traditional advertising, and is sometimes referred to as the rotten-apple theory of advertising [4]. The implication of this effect in the context of traditional advertising media is in the domain of public policy: it is used to justify adopting regulations against false advertising.

In the context of online advertising, however, there is much more a publisher can do to measure this type of externality and reward or punish advertisers based on whether they create positive or negative externality. Publishers such as Google or Yahoo often can track when a user revisits their website and clicks on an ad, and also whether an ad leads to a conversion or some action on the advertiser's site. Designing mechanisms to extract the relevant information from this wealth of data and use it to overcome the externality problem and maximize the efficiency of the system in the long run is an interesting research direction.


Learning externalities. Throughout this paper, we studied the winner determination problem with externalities, assuming that the parameters of the model - user preferences in our main model - are known to the algorithm. Learning these parameters given the history of choices made by the users, or designing experiments in order to learn these parameters remains open.


Diversity problem. It is known that having diversity among the set of web search results or among the set of products displayed on an electronic store front is valuable. There has been some effort on designing algorithms in these applications that give some weight to the diversity of the solution set (see, for example, [16]). However, it is not clear what is the right way to incorporate the diversity component in the objective. Note that in our model, optimizing for the value of solution in presence of externalities can automatically result in a diverse solution set. This is because advertisers that are similar to each other impose greater negative externality on each other (e.g., presumably an advertiser who sells Apple computers imposes little externality on one that sells the fruit). This suggests that our framework might be a good starting point for defining a diversity optimization problem that is based on economic principles.


Dating problem. As mentioned earlier, online dating services can also be considered in the framework of lead generation. Similar externalities exist in the online dating industry: sending a woman $ w$ on a date with a man $ m$ imposes a negative externality on all other men, since it decreases their chances with $ w$. Currently, online dating services take one of the two extremes of either allowing unrestricted search (i.e., a subscriber has access to the profiles of anyone who meets his or her criteria, and can contact them, which is the model adapted by Yahoo! Personals or match.com), or matching people one pair at a time (this is the model adapted by $ e$Harmony). Chen et al. [2] initiated the study of the $ e$Harmony model from a stochastic optimization point of view. An interesting direction for future research is to study this problem in a model with externalities in order to strike the right balance between these two extremes.

Bibliography

1
Aaron Archer and Eva Tardos.
Truthful mechanisms for one-parameter agents.
In IEEE Symposium on Foundations of Computer Science, pages 482-491, 2001.
2
Ning Chen, Nicole Immorlica, Anna Karlin, Mohammad Mahdian, and Atri Rudra.
Approximating matches made in heaven.
in preparation, 2008.
3
W. Gaertner.
Domain restrictions.
In K.J. Arrow, A.K. Sen, and K. Suzumura, editors, Handbook of Social Choice and Welfare, volume I, chapter 3, pages 131-170. Elsevier Science, 2002.
4
Z. K. Hansen and M. Law.
The political economy of truth-in-advertising regulation in the progressive era.
Forthcoming at the Journal of Law and Economics. An earlier version is available as NBER Working Paper No. 11927, 2006.
5
Philippe Jehiel and Benny Moldovanu.
Strategic non-participation.
Rand Journal of Economics, 27(1):84-98, 1996.
6
Philippe Jehiel and Benny Moldovanu.
Efficient design with interdependent valuations.
Econometrica, 69(5):1237-59, 2001.
7
Philippe Jehiel, Benny Moldovanu, and E. Stacchetti.
How (not) to sell nuclear weapons.
American Economic Review, 86(4):814-829, 1996.
8
Philippe Jehiel, Benny Moldovanu, and E. Stacchetti.
Multidimensional mechanism design for auctions with externalities.
Journal of Economic Theory, 85(2):258-294, 1999.
9
T. Joachims, L. Granka, Bing Pan, H. Hembrooke, F. Radlinski, and G. Gay.
Evaluating the accuracy of implicit feedback from clicks and query reformulations in web search.
ACM Transactions on Information Systems (TOIS), 25(2), April 2007.
10
Anshul Kothari, David C. Parkes, and Subhash Suri.
Approximately-strategyproof and tractable multiunit auctions.
Decision Support Systems, 39(1):105-121, 2005.
11
Internet Advertising Bureau.
Online lead generation: Standards and guidelines.
http://www.iab.net/standards/lead_generation.asp.
12
PricewaterhouseCoopers.
IAB Internet Advertising Revenue Report, 2006 Full-Year Results.
available at http://www.iab.net/resources/adrevenue/pdf/ IAB_PwC_2006_Final.pdf, May 2007.
13
Y. Sprumont.
The division problem with single-peaked preferences: a characterization of the uniform allocation rule.
Econometrica, 59(2):509-519, 1991.
14
J. Håstad.
Clique is hard to approximate within $ n^{1-\epsilon}$.
Acta Mathematica, 182:105-142, 1999.
15
Vijay V. Vazirani.
Approximation Algorithms.
Springer-Verlag, 2001.
16
Xiaojin Zhu, Andrew Goldberg, Jurgen Van Gael, and David Andrzejewski.
Improving diversity in ranking using absorbing random walks.
In Human Language Technologies: The Annual Conference of the North American Chapter of the Association for Computational Linguistics (NAACL-HLT), 2007.


Footnotes

... industry1
Another growing industry that can be studied in the framework of ``lead generation'' is online dating services. However, since currently the standard in this industry is based on flat-fee subscription and not pay-for-performance, our models might not be directly applicable.
....2
Note that for the purpose of solving the algorithmic question, having a prior knowledge of $ v_{\min}$ and $ R$ is not important, since these values can be computed from the input. However, doing so can violate the monotonicity property; for example, if the advertiser that has the minimum $ v_i$ increases her value, this changes the structure of the buckets and could result in decreasing her chance of getting selected.