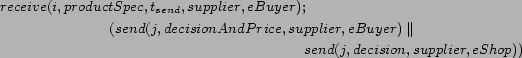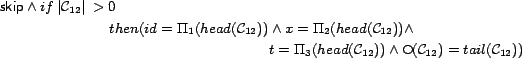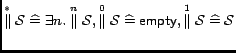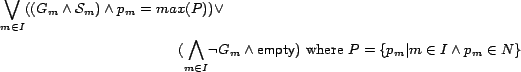Copyright is held by the World Wide Web Conference Committee (IW3C2).
Distribution of these papers is limited to classroom use, and personal use by others.
WWW 2006, May 23.26, 2006, Edinburgh, Scotland.
ACM 1-59593-323-9/06/0005.
ABSTRACT
A Service oriented system emerges from composition of services.
Dynamically composed reactive Web services form a special class
of service oriented system, where the delays associated with
communication, unreliability and unavailability of services,
and competition for resources from multiple service requesters
are dominant concerns. As complexity of services increase, an
abstract design language for the specification of services and
interaction between them is desired. In this paper, we present
ASDL (Abstract Service Design Language), a wide spectrum
language for modelling Web services. We initially provide an
informal description of our computational model for service
oriented systems. We then present ASDL along with its
specification oriented semantics defined in Interval Temporal
Logic (ITL): a sound formalism for specifying and reasoning
about temporal properties of systems. The objective of ASDL is
to provide a notation for the design of service composition and
interaction protocols at an abstract level.
Keywords
Abstract, Wide spectrum, Computational model, Web services, ASDL
![\includegraphics[scale=0.3]{/home/monika/Texfiles/figures/model/asdl}](5010-solanki-img6.png)
![\includegraphics[scale=0.5]{/home/monika/Texfiles/figures/model/failure_001}](5010-solanki-img10.png)
![\includegraphics[scale=0.5]{/home/monika/Texfiles/figures/model/failure_002}](5010-solanki-img11.png)