Budget Constrained Bidding in Keyword Auctions and Online Knapsack Problems

Yunhong Zhou

HP Labs

1501 Page Mill Rd

yunhong.zhou@hp.com

Deeparnab Chakrabarty¹ College of Computing

Georgia Tech

Atlanta, GA 30332

deepc@cc.gatech.edu

Rajan Lukose

HP Labs

1501 Page Mill Rd

rajan.lukose@hp.com

Categories and Subject Descriptors

General Terms

Keywords

Categories and Subject Descriptors: G.1.6 [Mathematics of Computing]: Mathematical Software - Algorithm Design and Analysis

Keywords: Sponsored search auction, keyword bidding, multiple-choice knapsack problem, stochastic optimization

Abstract:

We consider the budget-constrained bidding optimization problem for sponsored search auctions, and model it as an online (multiple-choice) knapsack problem. We design both deterministic and randomized algorithms for the online (multiple-choice) knapsack problems achieving a provably optimal competitive ratio. This translates back to fully automatic bidding strategies maximizing either profit or revenue for the budget-constrained advertiser. Our bidding strategy for revenue maximization is oblivious (i.e., without knowledge) of other bidders' prices and/or click-through-rates for those positions. We evaluate our bidding algorithms using both synthetic data and real bidding data gathered manually, and also discuss a sniping heuristic that strictly improves bidding performance. With sniping and parameter tuning enabled, our bidding algorithms can achieve a performance ratio above 90% against the optimum by the omniscient bidder.

1 Introduction

Keyword Bidding Models. For simplicity, assume that the default advertiser has a budget

over a fixed time horizon, discretized into time periods $1, \ldots, T$ . He is interested in a single keyword with expected value-per-click $\ensuremath{V}$ .

There are bidders $\{1,\cdots,N\}$ at time

for this keyword and their bids are sorted in decreasing order $b_1(t) > \ldots > b_N(t)$ . There are

ad slots, and are assigned to the top-

bids as follows: bidder

gets slot

; for each user click on his ad, bidder

is charged a price $b_{s+1}$ , if

or a minimum fee $b_{\min}$ (usually 10¢). Each slot $s$ has a click-through-rate (CTR), denoted $\alpha(s)$ , which is defined as the total number of clicks on an ad divided by the total number of impressions (displays). Therefore the default advertiser can obtain slot

by bidding slightly over

; for each user click, he incurs a cost of

, obtains an expected revenue $\ensuremath{V}$ and profit $\ensuremath{V}- b_s(t)$ .

Online Knapsack Problems. Let us start with the relatively simple single-slot case. At time

is the maximum bid among bidders

, and

is the number of clicks at period

. Winning at time

costs the advertiser

and earns him a profit of

where

Our Assumptions. In general, no online algorithm can achieve any non-trivial competitive ratio (the ratio between the output of the given algorithm and the offline optimum) for Online-KP [4]. Fortunately, in our setting, we make two reasonable assumptions on the knapsack items, which allow us to develop interesting online algorithms. These two assumptions are:

1 Our Results

In Section 3, we design both determinstic and randomized algorithms for the online knapsack problem, while both algorithms have competitive ratio $\ln(U/L) + 1$ .We also show a matching lower bound. Therefore our algorithm is provably optimal in the worst-case sense.

In Section 3.1, we translate the online knapsack algorithm into bidding strategies for the single-slot auction, for both profit and revenue maximization. In Section 4, we give a $(\ln(U/L)+2)$ -competitive online algorithm for the multiple-choice knapsack problem (MCKP)We translate the algorithm for Online-MCKP to bidding strategies for the multiple-slot case, and obtain both profit-maximizing and revenue-maximizing bidding strategies.

Our experimental work (restricted by limited evaluation data), reported in Section 5, suggests that two heuristics, sniping and parameter tuning, help to improve the performance of our bidding algorithms. With both sniping and parameter tuning enabled, our bidding algorithms (for both profit and revenue maximization) achieve an output value which is consistently more than 90% of the optimum by the omniscient bidder.

2 Related Work

Keyword Bidding. Sponsored search auctions have attracted a lot of attention, for both auctioneer revenue maximization and advertiser bidding optimization. Among all these work, Mehta etc al. [5] studied the auctioneer revenue maximization with budget-constrained bidders, using a trade-off function $\Psi$ (compare it to our threshold function) to grant queries to bidders, and the technique they use is probably most similar to the threshold function we use.

Online Algorithms. Awerbuch et al. [2] studied the online call routing which generalizes the online classical knapsack problem. More recently, Buchbinder et al. [3] designed online algorithms for fractional versions of general packing problems which imply an $O(\ln(U/L))$ -competitive algorithm for the online knapsack problem.

3 The Online Knapsack Problem

Randomized Algorithm: Let $\mathcal{D}$ be the continuous distribution from

, with the following density function: $f(x) = \frac{c}{x}$ , for $L \le x \le U$ , and

for $0 \le x \le L$ , where $c = \frac{1}{1+\ln(U/L)}$ Algorithm ONLINE-KP-RANDOMIZED simply picks a threshhold $\rho$ from the distribution $\mathcal{D}$ ; at each time, it picks item

iff its efficiency is at least $\rho$ and its budget allows.

Deterministic Algorithm: Our deterministic algorithm for Online-KP works against all adversaries..
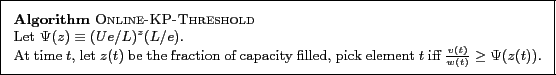
$\begin{framed} \noindent {\bf Algorithm} {\sc Online-KP-Threshold}\\ \noindent ... ...ent $t$\ iff $ \frac{{v}(t)}{w(t)} \ge \Psi(z(t)). \vspace{-1ex} $ \end{framed}$

1 Single-Slot Auctions

we can translate the algorithms ONLINE-KP-THRESHOLD to bidding strategies for single-slot keyword auctions for both profit and revenue maximization, based on Eq. (1). Details are omitted due to space constraints.

4 Online-MCKP & Multiple Slots

The Online-MCKP. The Online-MCKP is a generalization of the Online-KP. At each time period, at most one item can be selected from the item-set $N_t = \{(v_s(t), w_s(t))\}$ . The goal again is to maximize the total value of items selected.

The Algorithm Online-MCKP-Threshold is a generalization of Alg Online-KP-Threshold, and it works as follows: 1
$\begin{framed} \mbox{ \parbox[c]{15cm}{ \noindent {\bf Algorithm} {\sc Online-MC... ...Pick element $s \in E_t$\ with maximum ${v}_s(t)$. \end{itemize}} } \end{framed}$
Let $\Psi(z)$ and

be the same as before. At time

, let $E_t \equiv \left\{ s \in N_t \mid \frac{{v}_s(t)}{w_s(t)} \ge \Psi(z(t)) \right\}$ . If $E_t \neq \emptyset$ , pick element $s \in E_t$ with maximum ${v}_s(t)$ .

Multiple-Slot Bidding. Next we translate Alg. ONLINE-MCKP-THRESHOLD to bidding strategies for both profit and revenue maximization. It turns out the revenue maximization strategy is the same as the single-slot case, thus omitted. The profit-maximization bidding strategy is below:

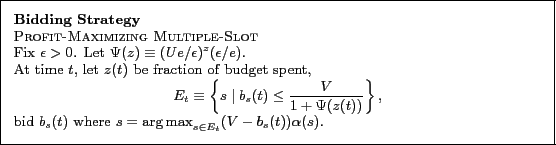
$\begin{framed} \noindent {\bf Bidding Strategy} \\ {\sc Profit-Maximizing Multi... ...(s = {\arg \max}_{s \in E_t} (\ensuremath{V}- b_s(t)) \alpha(s). \) \end{framed}$

5 Experimental Exploration

In this section, we evaluate our bidding algorithms using both synthetic and real-world data, and discuss two useful heuristics: sniping and parameter tuning.

The Sniping Heuristic. Simulation of the bidding algorithm described above with synthetic dataset shows that the bidding algorithm is too conservative, and leaves a significant fraction of budget unspent. Thus a potential performance improvement is sniping towards the end of the auction. If the bidder has knowledge (reliable estimates) about the click traffic (

) and the click-through rates, then the bidding strategies can be modified to increase its bid appropriately. Theoretically, we can prove that sniping strictly improve the performance of the algorithm. For details, see the technical report [6].

Parameter Tunning. If the lower bound $L$ in the online knapsack problem is too small, we can replace it with a larger value

for the threshold function $\Psi$ . This essentially discards items with very low efficiency, and the loss is minimal if the optimal solution consists of items with relatively high efficiency . It turns out tuning the parameter

makes a significant performance improvement.

Evaluation using Real Bidding Data. Next we report some experimental results on evaluating bidding algorithms for multiple-slot auctions using real bidding data. We scraped bidding data from the now defunct Overture webpage [1] with continous crawling for about two weeks, for one of the most dynamic and expensive keyword ``auto insurance.'' There are totally

distinct time periods in our collected data, and most top-5 bids are larger than $10. For the experiments, we use

, and three different values

. We evaluated both the profit-maximizing and revenue-maximizing strategies with and without sniping. For all these experiments, we use $U = V/b_{\min} - 1$ for profit maximization and $U = V/b_{\min}$ for revenue maximization, and $b_{\min} = 0.9$ .

Since results are very similar for different parameter values, we summarize them in Table 5. For all the examples we run, sniping improves the bidding performance significantly while exhausting the budget. Table 5 seems to tell us, for almost all values, with parameter tuning of

, the performance ratio ( $\rm {ALG}/\rm {OPT}$ ) is around 70%-75% without sniping, and 90%-95% with sniping.

Profit-Maximization Bidding Performance
V	OPT	ALG	ALG/	budget	ALG	ALG/
			OPT	left	(sniping)	OPT
8	3779	2751	73%	225.5	3541	94%
10	4974	4059	82%	116.1	4607	93%
12	6169	4463	72%	240.8	5842	95%

6 Concluding Remarks

We use worst-case competitive analysis, comparing our bidding strategy with the omniscient bidder who know everything in advance. In practice, other bidders do not behave in the worst-case but bid according to their own strategies. It would be interesting if one could attain bidding algorithms with better performance with the capabilities to learn other agents' bidding strategies or bidding price distributions. Incorporating previous work on stochastic knapsack problems together with average-case analysis (e.g. Lueker []) might be an essential ingredient. In a companion paper [], we try to address these problems.

There is a small gap of 1 in the lower and upper bounds for the competitive ratio of the Online-MCKP. As an open problem, it will be nice to close the gap.

Acknowledgement: We thank the following people for helpful discussions and feedback: Gagan Aggarwal, Terence Kelly, Victor Naroditskiy, Paul O'Brien, David Pennock, Jim Saxe and Bob Tarjan. We also thank an anonymous referee for suggesting randomized threshold algorithms.