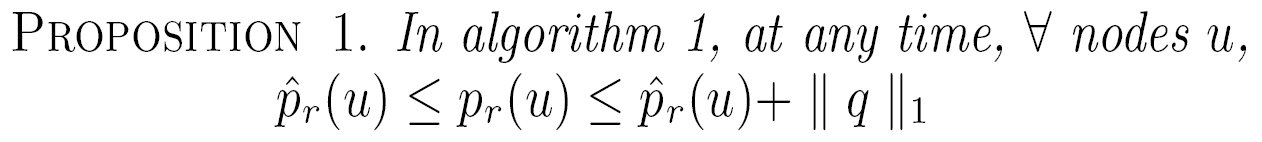
WeakestProp
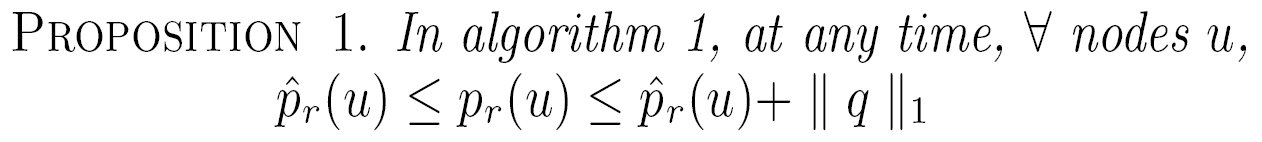
WeakestProp
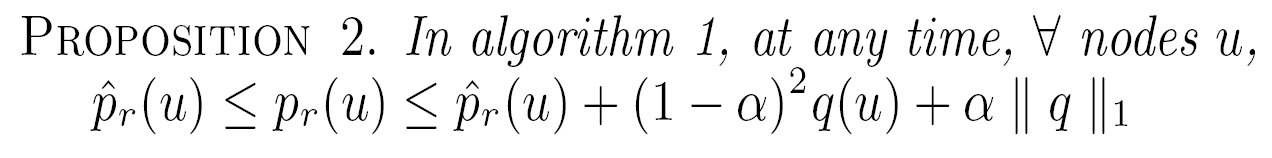
TheoreticalProp

Basic Push Algorithm
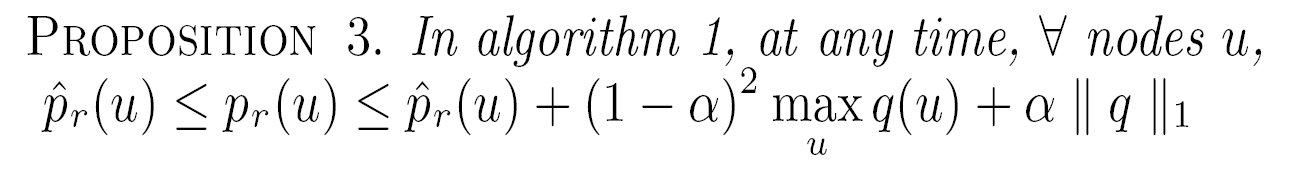
BestProp

Top-k termination check for Basic Push

Node Deletion Algorithm
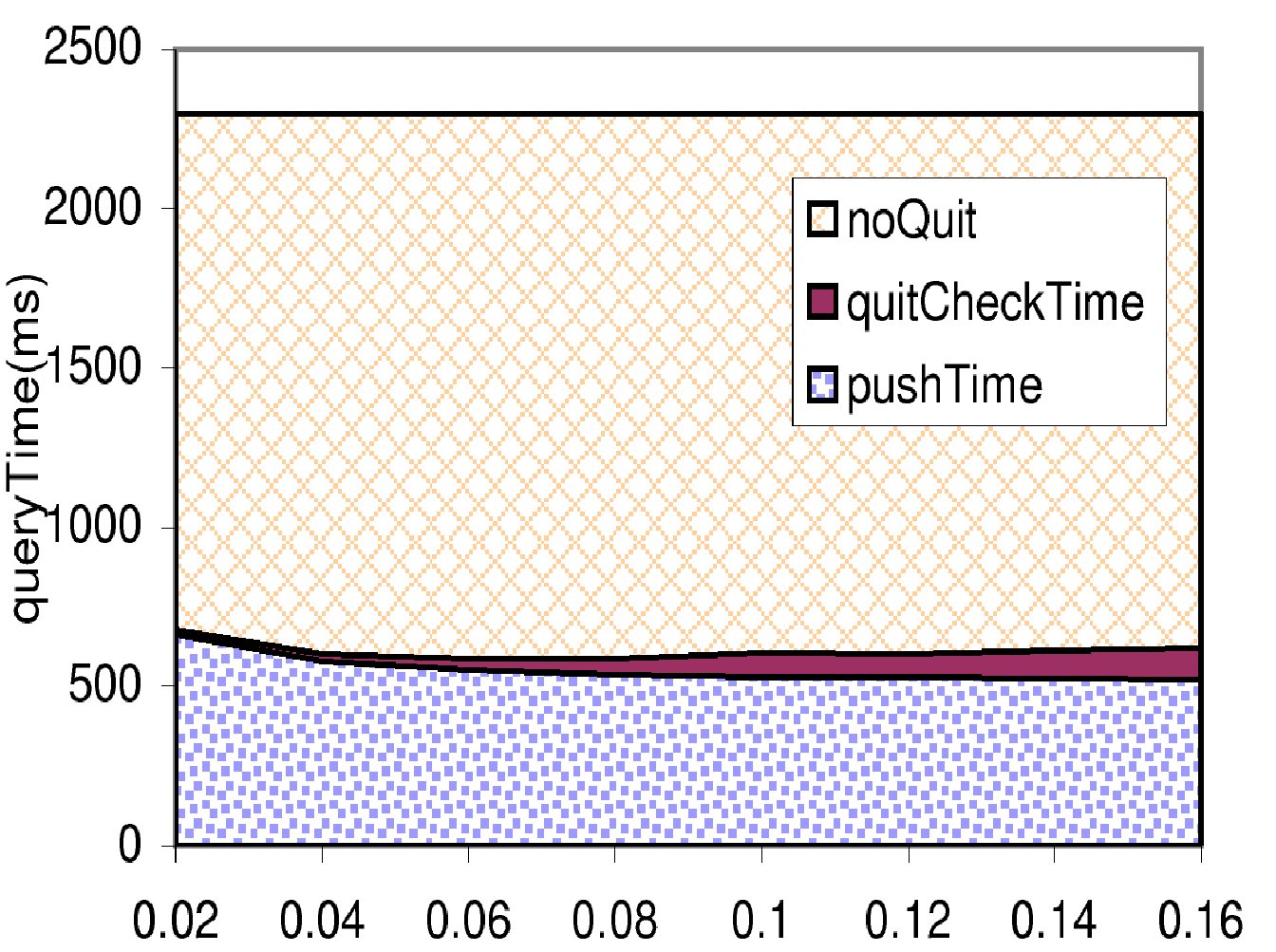
Push times averaged across queries vs. fraction of push time allowed in termination checks.(The top line uses no termination checks.)
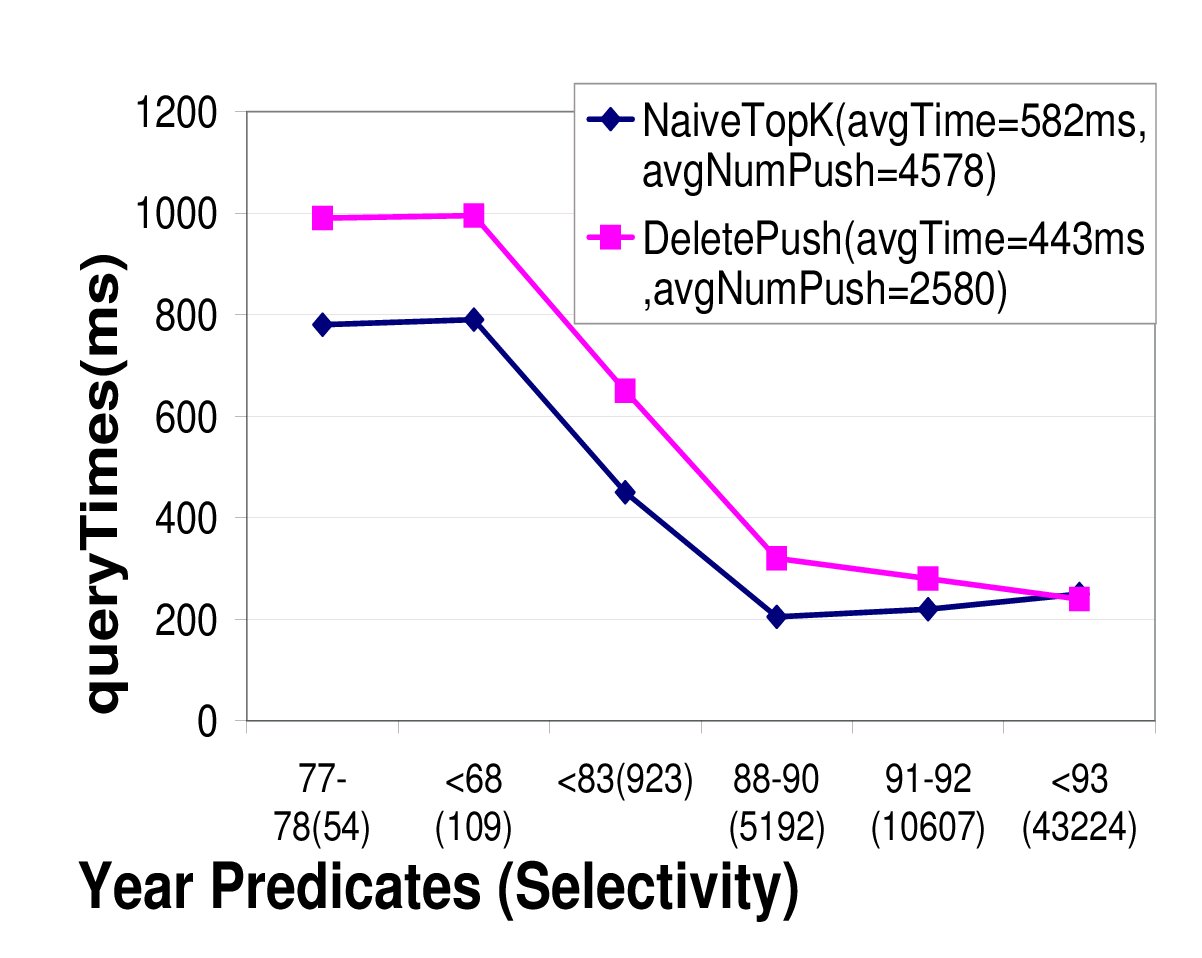
Comparison of top-k algorithms
[1] P. Berkhin. Bookmark-coloring approach to personalized pagerank computing. Internet Mathematics, 3(1):41-62, Jan. 2007.
[2] A. Z. Broder, R. Kumar, F. Maghoul, P. Raghavan, S. Rajagopalan, R. Stata, A. Tomkins, and J. L. Wiener. Graph structure in the web. Computer Networks, 33(1-6):309-320, 2000.
[3] S. Chakrabarti. Dynamic personalized PageRank in entity-relation graphs. In www, Banff, May 2007.
[4] G. Jeh and J. Widom. Scaling personalized web search. In WWW Conference, pages 271-279, 2003.
[5] S. D. Kamvar, T. H. Haveliwala, C. D. Manning, and G. H. Golub. Exploiting the block structure of the web for computing, Mar. 12 2003