WWW 2008, April 21-25, 2008, Beijing, China. 2008 978-1-60558-085-2/08/04

2

Algorithm for Stochastic Multiple-Choice Knapsack Problem and Application to Keywords Bidding

Yunhong Zhou

HP Labs

1501 Page Mill Rd

yunhong.zhou@hp.com

Victor Naroditskiy ¹

Department of Computer Science

Brown University

victor@brown.edu

Abstract:

We model budget-constrained keyword bidding in sponsored search auctions as a stochastic multiple-choice knapsack problem (S-MCKP) and design an algorithm to solve S-MCKP and the corresponding bidding optimization problem. Our algorithm selects items online based on a threshold function which can be built/updated using historical data. Our algorithm achieved about 99% performance compared to the offline optimum when applied to a real bidding dataset. With synthetic dataset and iid item-sets, its performance ratio against the offline optimum converges to one empirically with increasing number of periods.

Categories and Subject Descriptors

G.1.6 [Mathematics of Computing]: Numerical Analysis - Optimization (stochastic programming)

General Terms

Algorithms, Economics

Keywords

Sponsored search auction, keyword bidding, multiple-choice knapsack problem, stochastic optimization

1 Introduction

Sponsored search auction is an effective way of monetizing search activities where advertisers pay to place their ads on search results pages for specific user keyword queries. In this work we focus on the bidding optimization problem for an advertiser with budget constraints. Formally, we address the following problem: for each keyword and each time period, how much should the advertiser bid (i.e., which position to obtain), so as to maximize ROI of the ads given a fixed budget and a fixed time horizon?

We can view each ad position as an item with associated weight (cost) and value (either revenue or profit). The advertiser has a budget constraint, and it naturally corresponds to the knapsack capacity. Furthermore each advertiser can have at most one ad appear on each keyword results page. This corresponds to the constraint that at most one item from each item-set can be taken in the multiple-choice knapsack problem (MCKP), a well-known variation of the knapsack problem (KP). The following model of the bidding problem is proposed: given multiple keywords $k \in K$, multiple time periods when the advertiser places bids $t \in \{1, \ldots, T\}$, and multiple positions $s \in \{1, \ldots, S\}$, the item-set $N^k_{t}$ consists of items $(w^k_{ts}, v^k_{ts})$ for all ad positions s. Formally $w^k_{ts}$ and $v^k_{ts}$ are defined as follows:

$$w^k_{ts} = p^k_{ts} \alpha^k(s) X^k(t),$$

$$v^k_{ts} = (V^k - p^k_{ts}) \alpha^k(s) X^k(t),  \forall s, t, k.$$ (1)

Here $V^k$ denotes the expected value-per-click for keyword $k$, $X^k(t)$ denotes the number of user queries for keyword $k$ at time period $t$, $\alpha^k(s)$ denotes the click-through rate (CTR) of position $s$ and keyword $k$ (the ratio between total user clicks on the ad at $s$-th slot and the total number of impressions), and $p^k_{ts}$ denotes the cost-per-click for ads in position $s$ for keyword $k$ at time $t$.

The bidding optimization problem has a strong stochastic flavor as bidding prices and click traffic change all the time. The online and stochastic variant of MCKP (S-MCKP) where item-sets are received one at a time, allows us to explicitly incorporate this uncertainty in the distribution of future item-sets. Although, decisions are made assuming that the item-sets are independent and identically distributed (iid), the algorithm performs well even when items in different time periods do not follow the same distribution as evidenced by experimental results for the ``auto insurance" dataset.

1 Related Work

In the last few years, a number of papers addressed the problem of revenue maximization or bidding optimization in sponsored search auctions [1,4,2,3,7]. None of the previous work proposed a solution that employs distributional information about prices and solves the bidding problem with multiple ad position, keywords, and time periods. Zhou et al. [8] attack a very similar problem and model it as Online-MCKP; however their work focuses on competitive algorithms with worst-case performance guarantees while this work focuses on average-case performance with stochastic input. The threshold function we develop for S-MCKP is based on the threshold function for the stochastic knapsack problem by Lueker [6].

2 Approximating S-MCKP

Our algorithm for the S-MCKP is based on Lueker's Algorithm for Online-KP and an approximation for MCKP [5]. At a high level, we use a technique from the approximation for MCKP to convert each MCKP item-set into KP items and apply Lueker's threshold function to selected KP items. We now describe the algorithm in detail.

We first apply a technique for converting items from a MCKP item-set into incremental items with the following property: taking multiple incremental items with decreasing efficiency (value/weight) is equivalent to taking exactly one original item. The technique consists of two steps: (i) removing dominated and LP-dominated items from the item-set and (ii) creating incremental items from undominated items. For details, see Kellerer et al. [5], p.320.

After obtaining incremental items, we use a threshold function to decide which incremental items to take. Lueker [6] proposed solving Online-KP using an adaptive threshold: only items that meet the threshold efficiency are put in the knapsack. The threshold function (which we call $g$) maps the average remaining capacity per time period to the threshold efficiency $e^*$. The threshold efficiency is such that the expected weight of the remaining items (all items are iid) with efficiency at least $e^*$ is equal to the remaining capacity:

$$C = \text{E}_{w,v} \left[ \sum_{i=1}^n w_i \:\mathbf{1}_{\{\frac{... ...t] \:=\: n  \text{E}_{w,v} \left[w\:\mathbf{1}_{\{\frac{v}{w} \ge e^*\}}\right]$$

$$f(e^*) \:=\: \frac{C}{n} \quad \text{while}\quad f(e) \:\equiv\: \text{E}_{w,v} \left[ w\:\mathbf{1}_{\{\frac{v}{w} \ge e\}}\right]$$ (2)

We need the distribution of incremental items to calculate the threshold function (Eq. 2), however such information may not be known or have a closed-form representation. Alternatively, we can approximate the threshold function of incremental items using item-sets received in the past. Formally, given a sample set of $m$ incremental items, we can use $\tilde{f}$ to approximate $f$ where

$$\vspace{-1ex} \tilde{f}(e) \:\equiv\: \frac{1}{m} \sum_{i=1}^m w_i\:\mathbf{1}_{\{\frac{v_i}{w_i} \ge e\}}$$ (3)

$\tilde{f}$ is a piecewise constant function with at most $m$ pieces, and it can be computed in time $O(m \log m)$ based on sorting of item efficiency.

The algorithm for S-MCKP is in Figure 1. It consists of two phases: the first phase (optional) is to generate the threshold function if training item-sets are available. In the second phase, at each time period the algorithm converts the current item-set to incremental items, checks which incremental items meet the threshold, and takes the corresponding item from the item-set. The threshold function can be updated in step 2 by incorporating information from the current item-set. In the case when no training item-sets are available in step 1, the first real item-set is used to generate the initial threshold function.

Figure 1: Algorithm for S-MCKP.

3 Experimental Results

We run two sets of experiments. In the first set of experiments, we generate items with weights and values drawn independently from one of the following distributions: Uniform with support between 1 and 10, Normal with mean 10, and Exponential with mean 10. The number of items per set received each time period is 5. We express the budget (capacity) as a fraction of the mean weight of an item times the total number of time periods, i.e., $C = \lambda \times n \times \textrm{mean}(w)$, where $n$ is the number of time periods, $\textrm{mean}(w)$ is the mean weight of a random item. The value of $\lambda$ indicates whether the budget is large compared to the expected overall spending if you pick random items each time without any optimization. We tested the algorithms on problem instances with the budget level $\lambda \in \{0.05, 0.2, 0.5, 0.9, 1.1\}$.

We evaluate the performance of the algorithm based on the ratio of the value obtained by the algorithm and an upper bound on the optimal solution to offline MCKP. Results below are for the experiment with no training item-sets for generating the threshold function in step 1 of Alg 1. The performance of the algorithm is almost always within 10% of the optimal when $n \ge 20$ and approaches the optimal as $n$ goes to $\infty$. A graph for the performance of Alg 1 with the Uniform distribution is shown below. Graphs with the other distributions look very similar, and are omitted due to space constraints.

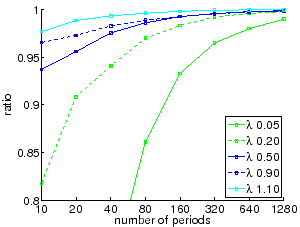
The second set of experiments uses a real dataset for the ``auto insurance" keyword described in [8]. The performance of our algorithm is around 99% while the algorithm in [8] achieves around 90%-95%.

Bibliography

1

Z. Abrams.
Revenue maximization when bidders have budgets.
In SODA, pages 1074-1082. ACM Press, 2006.

2

Z. Abrams, O. Mendelevitch, and J. A. Tomlin.
Optimal delivery of sponsored search advertisements subject to budget constraints.
In ACM EC, pages 272-278, 2007.

3

C. Borgs, J. Chayes, O. Etesami, N. Immorlica, K. Jain, and M. Mahdian.
Dynamics of bid optimization in online advertisement auctions.
In Proc. WWW, pp 531-540, 2007.

4

N. Buchbinder, K. Jain, and J. S. Naor.
Online primal-dual algorithms for maximizing ad-auctions revenue.
In Proc. ESA, pages 253-264, 2007.

5

H. Kellerer, U. Pferschy, and D. Pisinger.
Knapsack Problems.
Springer, 2004.

6

G. S. Lueker.
Average-case analysis of off-line and on-line knapsack problems.
J. of Algorithms, 29(2):277-305, 1998.

7

S. Muthukrishnan, M. Pál, and Z. Svitkina.
Stochastic models for budget optimization in search-based advertising.
In Proc. WINE, LNCS 4858, pages 131-142, 2007.

8

Y. Zhou, D. Chakrabarty, and R. Lukose.
Budget constrained bidding in keyword auctions and online knapsack problems.
In Proc. WWW (poster), 2008.

Footnotes

... Naroditskiy ¹

Work was done while the author was an intern at HP Labs.