Nowadays OWL[22] has been established as a
core standard in the Semantic Web. It comes in three layers in
ascending expressivity, i.e., OWL Lite, OWL DL and OWL Full,
where the former two coincide semantically with certain
description logics (DLs) [1].
A DL-based ontology consists of an intensional part and an
extensional part. The intensional part consists of a TBox
and an RBox, and contains knowledge about concepts and relations
(called roles) between the elements of the domain. The
extensional part consists of an ABox, and contains
knowledge about individuals and how they relate to the concepts
and roles from the intensional part. In this paper, the knowledge
in intensional parts is called axioms, whilst the
knowledge in extensional parts is called ABox assertions
or simply assertions.
A crucial question in the vision of Semantic Web is how to
support and ease the process of creating and maintaining DL-based
ontologies. An important task within this process is ontology
population, which adds instances of concepts and relations to
the ontology. In recent years, there has been a great surge of
interest in methods for populating ontologies from textual
resources. To name a few, Text2Onto [3] and KITE [30] are frameworks that integrate
algorithms for populating ontologies from textual data. The
algorithms include information extraction algorithms that assign
annotations carrying some semantics to regions of the data, and
co-reference algorithms that identify annotated individuals in
multiple places. As for populating DL-based ontologies, the
information extraction process behaves as adding concept/role
assertions, whilst the co-reference process behaves as adding
equality/inequality assertions. The populated ontology, however,
may become inconsistent because the information
extraction/co-reference process is imprecise or the populated
data possibly conflict with the original data. In order to repair
the populated ontology, we propose to delete a subset of
assertions in which the sum of removal costs is minimum, based on
the following considerations. First, the intensional part should
not be changed, because in general it is well prepared and
coherent (i.e., having no unsatisfiable concepts) before
the population. Second, for changing the extensional part, only
the deletion of assertions is considered because there is
generally no criteria for revising assertions. Third, for
deleting assertions, some minimal criteria on removable
assertions (e.g., the cost of losing information) should be
considered. Fourth, the certainty information on an assertion,
given by the information extraction/co-reference process, can be
used as the cost of losing information (called the removal
cost), because deleting a more certain assertion generally
loses more information. Fifth, the collective removal cost of a
set of assertions can be approximated by the sum of removal costs
in the set.
Therefore, we in this paper address computing a minimum
cost diagnosis for an inconsistent ontology  , i.e. a subset of removable assertions whose
removal turns
, i.e. a subset of removable assertions whose
removal turns  consistent and in which
the sum of removal costs is minimum. We show that, unless P=NP,
the problem of finding a minimum cost diagnosis for a DL-Lite
ontology is insolvable in polynomial time (PTIME) w.r.t. data
complexity, i.e. the complexity measured in the size of the ABox only.
Note that DL-Lite is a fairly inexpressive DL language such that
the consistency checking problem for DL-Lite ontologies is in
PTIME in the size of the ontology [2]. This complexity result implies
that the problem of finding minimum cost diagnoses is in general
intractable. In spite of that, we develop a feasible
computational method for more general (i.e.
consistent and in which
the sum of removal costs is minimum. We show that, unless P=NP,
the problem of finding a minimum cost diagnosis for a DL-Lite
ontology is insolvable in polynomial time (PTIME) w.r.t. data
complexity, i.e. the complexity measured in the size of the ABox only.
Note that DL-Lite is a fairly inexpressive DL language such that
the consistency checking problem for DL-Lite ontologies is in
PTIME in the size of the ontology [2]. This complexity result implies
that the problem of finding minimum cost diagnoses is in general
intractable. In spite of that, we develop a feasible
computational method for more general (i.e.
 ) ontologies. It
transforms a
) ontologies. It
transforms a
 ontology to a set
of disjoint propositional programs by applying an existing
transformation method (from
ontology to a set
of disjoint propositional programs by applying an existing
transformation method (from
 to disjunctive
datalog) [12,21] and new grounding and partitioning
techniques. Thus our method reduces the problem of finding a
minimum cost diagnosis into a set of independent subproblems.
Each such subproblem computes an optimal model and is solvable in
to disjunctive
datalog) [12,21] and new grounding and partitioning
techniques. Thus our method reduces the problem of finding a
minimum cost diagnosis into a set of independent subproblems.
Each such subproblem computes an optimal model and is solvable in
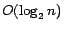 calls to a
satisfiability (SAT) solver, by assuming that removal costs have
been scaled to positive integers polynomial in
calls to a
satisfiability (SAT) solver, by assuming that removal costs have
been scaled to positive integers polynomial in 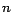 the number of removable assertions.
the number of removable assertions.
We implement our method and experiment on several originally
consistent, real/benchmark ontologies. Each test ontology has
over thousands of assertions. We implement a tool to inject
conflicts into a consistent ontology, where a conflict, caused by
several inserted assertions, violates a functional restriction or
a disjointness constraint. Experimental results show that, even
when all assertions are assumed removable, our method can handle
all the test ontologies with injected conflicts. Especially, our
method scales well on the extended benchmark ontologies with
increasing number (from 1000) of conflicts.
There are some works that address repairing DL-based
ontologies. Kalyanpur et al. [13] extended Reiter's Hitting Set Tree
(HST) algorithm [24] to compute
a minimum-rank hitting set, which is a subset of axioms that need
to be removed/fixed to correct an unsatisfiable concept, such
that the sum of axiom ranks in the subset is minimum. The notion
of minimum-rank hitting set is similar to that of minimum cost
diagnosis, except that the former is on axioms while the latter
is on assertions. Schlobach [26] applied Reiter's HST algorithm to
compute a minimal subset of axioms that need to be removed/fixed
to correct an unsatisfiable concept or an incoherent TBox. The
above methods require all minimal conflict sets be computed
beforehand, where a minimal conflict set is a minimal
subset of axioms responsible for the unwanted consequence. Though
the above methods can work with ABoxes as well (by viewing
assertions as axioms), it is impractical to adapt them to
computing minimum cost diagnoses. First, the problem of finding a
minimum hitting set from minimal conflict sets is intrinsically
intractable [15]. Second,
though there exist efficient methods for computing a minimal
conflict set (e.g., [27,14,20]), computing all minimal conflict
sets is still hard because the number of minimal conflict sets
can be exponential in the number of assertions, as shown in the
following example.
Example
1 Let the intensional part consist of two axioms
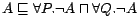
and
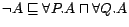
, and the
ABox be
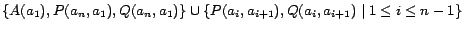
,
where
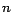
is an odd number. Then the
ontology is inconsistent, because
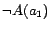
is one of its consequences but conflicts
with
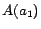
. The minimal conflict
sets over the ABox are of the form
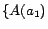
,
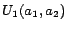
,
...,
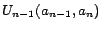
,
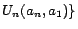
, where
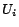
is either

or
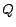
. So the number
of minimal conflict sets is
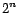
.
Hence, a method that computes minimum cost diagnoses from
minimal conflict sets may work in exponential time and
exponential space w.r.t. data complexity (e.g., when it handles
an ontology that is the union of the ontology in the above
example and the ontology given in the proof of Theorem 2). In contrast, our method
works in exponential time (more precisely, in logarithmic calls
to an NP oracle) and polynomial space w.r.t. data complexity.
There exist some heuristics-based methods for repairing
DL-based ontologies. Schlobach [25] proposed an approximate approach
to computing a subset of axioms whose removal corrects an
unsatisfiable concept or an incoherent TBox. Dolby et al.
[4] exploited summarization and
refinement techniques to compute a subset of assertions whose
removal turns an inconsistent ontology consistent. Their proposed
methods, however, cannot guarantee minimality for the set of
removed axioms/assertions.
There also exist some methods for revising problematic axioms
(e.g., [19,13,16,23]). But they cannot be adapted to
revising assertions, because assertions are assumed atomic in our
work. We only consider the deletion of assertions.
As for dealing with inconsistency in DL-based ontologies,
there is another approach that simply avoids/tolerates the
inconsistency and applies a non-standard reasoning method to
obtain meaningful answers (e.g., [11,17]). We can also adapt our method to
this approach, by defining a consistent consequence of an
inconsistent ontology as a consequence invariant under all
minimum cost diagnoses. This is out of the scope of this paper
and is not discussed here.
The
 description logic
[10] is a syntactic variant of
OWL DL [22] without nominals
and concrete domain specifications, but allowing qualified number
restrictions.
description logic
[10] is a syntactic variant of
OWL DL [22] without nominals
and concrete domain specifications, but allowing qualified number
restrictions.
A
 RBox
RBox
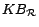 is a finite set of
transitivity axioms
is a finite set of
transitivity axioms 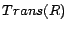 and role inclusion axioms
and role inclusion axioms
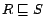 , where
, where  and
and 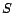 are roles. Let
are roles. Let 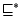 be the
reflexive transitive closure of
be the
reflexive transitive closure of
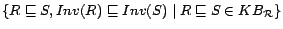 ,
where
,
where 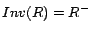 and
and 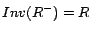 for a role
for a role  .
A role
.
A role 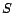 is simple if there is no
role
is simple if there is no
role  such that
such that
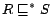 and either
and either
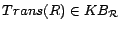 or
or
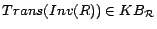 .
The set of
.
The set of
 concepts is the
smallest set containing
concepts is the
smallest set containing 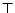 ,
,
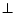 ,
, 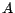 ,
,
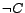 ,
,  ,
, 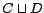 ,
,
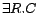 ,
, 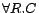 ,
, 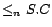 and
and 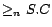 , where
, where 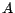 is a concept name (i.e. an atomic concept),
is a concept name (i.e. an atomic concept),
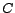 and
and 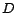
 concepts,
concepts,
 a role,
a role, 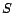 a simple role, and
a simple role, and 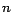 a
positive integer. A
a
positive integer. A
 TBox
TBox
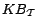 is a finite set of
concept inclusion axioms
is a finite set of
concept inclusion axioms
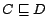 , where
, where 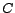 and
and 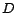 are
are
 concepts. A
concepts. A
 ABox
ABox
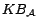 is a set of
concept assertions
is a set of
concept assertions 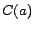 ,
role assertions
,
role assertions 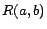 ,
equality assertions
,
equality assertions 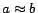 and inequality assertions
and inequality assertions
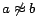 , where
, where 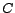 is a
is a
 concept,
concept,
 a role, and
a role, and 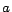 and
and 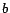 individuals. A
individuals. A
 ontology
ontology
 is a triple
is a triple
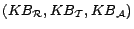 , where
, where
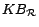 is an RBox,
is an RBox,
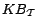 a TBox, and
a TBox, and
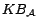 an ABox. In this
paper, by
an ABox. In this
paper, by  we simply denote
we simply denote
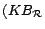 ,
,
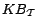 ,
,
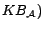 if there is no
confusion.
if there is no
confusion.
DL-Lite [2] is a
sub-language of
 . The set of DL-Lite
concepts is the smallest set containing
. The set of DL-Lite
concepts is the smallest set containing 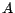 ,
, 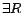 ,
, 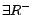 ,
, 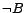 and
and 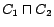 , where
, where 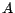 is a concept name,
is a concept name,  a role name,
a role name, 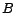 a basic concept (i.e. a concept of the form
a basic concept (i.e. a concept of the form
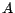 ,
, 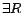 or
or 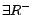 ), and
), and
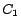 and
and 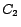 DL-Lite concepts.
DL-Lite concepts. 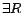 is actually an unqualified existential restriction
is actually an unqualified existential restriction
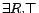 . A DL-Lite
ontology
. A DL-Lite
ontology
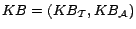 consists of a TBox
consists of a TBox
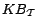 and an ABox
and an ABox
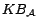 .
.
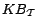 is a finite set of
inclusion axioms
is a finite set of
inclusion axioms
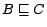 and
functionality axioms
and
functionality axioms
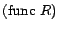 and
and
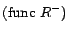 , where
, where
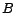 is a basic concept,
is a basic concept, 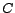 a DL-Lite concept and
a DL-Lite concept and
 a role.
a role.
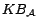 is a set of
concept assertions
is a set of
concept assertions 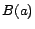 and
role assertions
and
role assertions 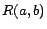 , where
, where
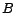 is a basic concept,
is a basic concept,  a role, and
a role, and 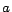 and
and 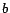 individuals.
individuals.
The semantics of a
 ontology
ontology
 is given by a mapping
is given by a mapping
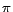 that translates
that translates  into first-order logic. Due to
space limitation, we refer readers to [12] for the definition of
into first-order logic. Due to
space limitation, we refer readers to [12] for the definition of 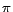 .
.  is said to be consistent/satisfiable if there exists a
first-order model of
is said to be consistent/satisfiable if there exists a
first-order model of 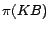 . The
semantics of a DL-Lite ontology
. The
semantics of a DL-Lite ontology  can still be given by the same mapping
can still be given by the same mapping 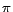 , because a functionality axiom
, because a functionality axiom
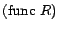 is a syntactic
variant of
is a syntactic
variant of
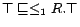 .
Note that the unique name assumption (UNA) [1] on individuals is applied in
DL-Lite but not in
.
Note that the unique name assumption (UNA) [1] on individuals is applied in
DL-Lite but not in
 . UNA can be
explicitly axiomatized by appending to the ABox all inequality
assertions
. UNA can be
explicitly axiomatized by appending to the ABox all inequality
assertions
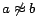 for any two
individuals
for any two
individuals 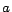 and
and 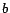 that have different URIs.
that have different URIs.
In our work we assume that all concept assertions are attached
to atomic concepts only, due to the following reasons. First, the
representation of non-atomic concept assertions is not supported
by the RDF/XML syntax of OWL (cf. http://www.w3.org/TR/owl-ref), which is the
main syntax for representing DL-based ontologies nowadays.
Second, a non-atomic concept assertion 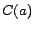 can be reduced to an atomic one by replacing
can be reduced to an atomic one by replacing
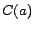 with
with 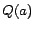 and appending
and appending 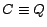 to the TBox, where
to the TBox, where 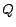 is a new atomic
concept.
is a new atomic
concept.
A disjunctive datalog program with equality [6]  is a
finite set of rules without function symbols of the form
is a
finite set of rules without function symbols of the form
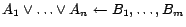 (where
(where
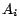 and
and 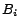 are atoms). Each rule must be safe, i.e., each
variable occurring in a head atom
are atoms). Each rule must be safe, i.e., each
variable occurring in a head atom 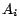 must occur in some body atom
must occur in some body atom 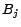 . For
a rule
. For
a rule 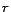 , the set of head atoms is
denoted by
, the set of head atoms is
denoted by 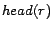 , whereas the set of
body atoms is denoted by
, whereas the set of
body atoms is denoted by 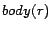 .
A rule
.
A rule 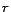 is called a constraint
if
is called a constraint
if 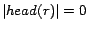 ; a
fact if
; a
fact if 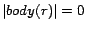 . An
atom is called negated if it leads with
negation-as-failure. Typical definitions of a disjunctive datalog
program, such as [6], allow
negated atoms in the body. In our work, negated atoms cannot
occur in a transformed program that we consider, so we omit
negation-as-failure from the definitions. Disjunctive datalog
programs without negation-as-failure are often called positive
programs.
. An
atom is called negated if it leads with
negation-as-failure. Typical definitions of a disjunctive datalog
program, such as [6], allow
negated atoms in the body. In our work, negated atoms cannot
occur in a transformed program that we consider, so we omit
negation-as-failure from the definitions. Disjunctive datalog
programs without negation-as-failure are often called positive
programs.
The set of all ground instances of rules in  is denoted by
is denoted by 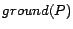 . An interpretation
. An interpretation 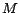 of
of  is a subset of
ground atoms in the Herbrand base of
is a subset of
ground atoms in the Herbrand base of  .
An interpretation
.
An interpretation 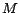 is called a
model of
is called a
model of  if (i)
if (i)
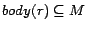 implies
implies
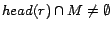 for
each rule
for
each rule
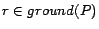 , and (ii) all
atoms from
, and (ii) all
atoms from 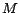 with the equality predicate
with the equality predicate
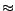 yield a congruence
relation, i.e. a relation that is reflexive, symmetric,
transitive, and
yield a congruence
relation, i.e. a relation that is reflexive, symmetric,
transitive, and
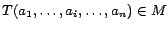 and
and
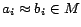 imply
imply
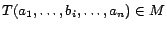 for each predicate symbol
for each predicate symbol 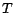 in
in
 .
.  is said to be satisfiable if it has a model.
is said to be satisfiable if it has a model.
Since
 is a subset of
first-order logic,
is a subset of
first-order logic,
 axioms can first be
translated into logical formulas, then into clausal form. The
resulting clauses can be represented as disjunctive rules without
negation-as-failure. However, due to possible skolemization steps
in the clausal form translation, the resulting rules may contain
function symbols. Standard logic program engines, however, may
not terminate in the presence of function symbols. To cope with
this problem, Hustadt et al. [12,21] developed the KAON2
transformation method to get rid of function symbols without
losing ABox consequences.
axioms can first be
translated into logical formulas, then into clausal form. The
resulting clauses can be represented as disjunctive rules without
negation-as-failure. However, due to possible skolemization steps
in the clausal form translation, the resulting rules may contain
function symbols. Standard logic program engines, however, may
not terminate in the presence of function symbols. To cope with
this problem, Hustadt et al. [12,21] developed the KAON2
transformation method to get rid of function symbols without
losing ABox consequences.
The method reduces a
 ontology
ontology
 to a positive disjunctive
datalog program
to a positive disjunctive
datalog program
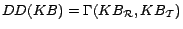
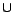
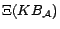
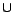
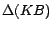 .
.
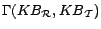 is a set of
disjunctive datalog rules computed from the intensional part of
is a set of
disjunctive datalog rules computed from the intensional part of
 by translating
by translating
 axioms into
clauses, adding logical consequences, and translating clauses
into disjunctive datalog rules.
axioms into
clauses, adding logical consequences, and translating clauses
into disjunctive datalog rules.
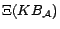 is a set of
facts translated from
is a set of
facts translated from
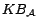 , where each
inequality assertion (of the form
, where each
inequality assertion (of the form
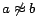 ) is translated
into a ground constraint (of the from
) is translated
into a ground constraint (of the from
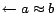 ), and other
assertions are directly translated into ground facts.
), and other
assertions are directly translated into ground facts. 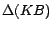 is a set of facts of
the form
is a set of facts of
the form 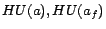 and
and 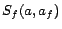 , which are introduced
to remove function symbols and instantiated for each individual
, which are introduced
to remove function symbols and instantiated for each individual
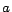 occurring in
occurring in  and each function symbol
and each function symbol 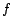 .
.
Theorem 1 ([
21]) For

a

ontology,

is unsatisfiable if and only
if
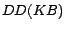
is unsatisfiable.
Given a possibly inconsistent
 ontology
ontology
 in which some assertions are
removable and assigned removal costs, our goal is to find a
subset of removable assertions whose removal turns
in which some assertions are
removable and assigned removal costs, our goal is to find a
subset of removable assertions whose removal turns  consistent and in which the sum
of removal costs is minimum. Such subset is called a minimum
cost diagnosis, formally defined below.
consistent and in which the sum
of removal costs is minimum. Such subset is called a minimum
cost diagnosis, formally defined below.
Definition
1 Let

be a possibly
inconsistent

ontology and
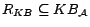
a set of removable assertions such that each assertion
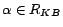
is given a
removal cost 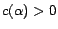
.
Then, a subset of assertions
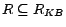
is called a
diagnosis for

w.r.t.
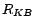
if
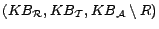
is consistent. A diagnosis

is
called a
minimum cost diagnosis for

w.r.t.
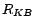
if there
is no diagnosis
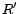
for

w.r.t.
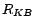
such that
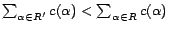
.

is simply called a
diagnosis/minimum cost diagnosis if

and
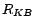
are clear from the
context.
We consider the time complexity for finding a minimum cost
diagnosis. Complexity results in this paper refer to data
complexity, i.e. the complexity measured as a function of the
number of assertions in the ontology. Theorem 2 shows that, unless P=NP,
there is no polynomial time algorithm for finding a minimum cost
diagnosis for a DL-Lite ontology  w.r.t.
w.r.t.
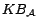 . It implies that
the problem of finding minimum cost diagnoses for
. It implies that
the problem of finding minimum cost diagnoses for
 ontologies is in
general intractable.
ontologies is in
general intractable.
Theorem
2 Given a positive integer
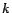
and a possibly inconsistent DL-Lite ontology
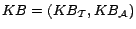
where each assertion
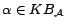
is
given a removal cost
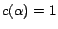
,
deciding if there is a diagnosis

for

w.r.t.
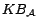
such that
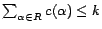
is NP-hard w.r.t. data
complexity.
Proof. Given an arbitrary instance 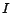 of the SAT problem, we transform it into an instance
of the SAT problem, we transform it into an instance
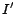 of the given decision
problem. Let
of the given decision
problem. Let 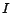 be the formula
be the formula
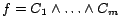 with
with
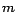 clauses and
clauses and 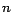 boolean variables
boolean variables
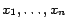 . We construct
. We construct
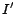 as follows. (1)
as follows. (1)
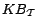 consists of the
following axioms:
consists of the
following axioms:
(2) For each boolean variable
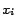
in
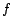
,
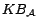
contains a
corresponding constant
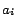
. (3) For each
clause
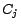
containing
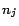
literals
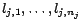
whose
corresponding constants in
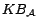
, introduced in
(2), are
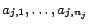
respectively,
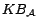
contains a
corresponding constant
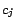
for
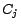
and
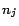
assertions
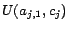
, ...,
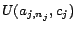
, where
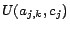
is
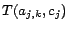
if
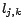
is positive, or
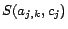
otherwise. (4)
Let
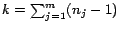
.
Now we prove that 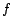 is satisfiable
if and only if there is a diagnosis
is satisfiable
if and only if there is a diagnosis  for
for
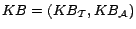 w.r.t.
w.r.t.
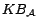 such that
such that
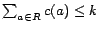 , i.e.,
, i.e.,
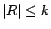 . (
. ( ) Since
) Since  is satisfiable, for each
clause
is satisfiable, for each
clause 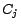 there is a literal
there is a literal
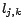 assigned
assigned 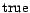 . We append to
. We append to  all assertions in
all assertions in
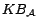 of the form
of the form
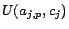 (
(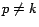 ), where
), where
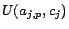 is
is
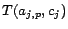 if
if 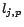 is positive, or
is positive, or
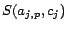 otherwise.
Clearly,
otherwise.
Clearly,  is a diagnosis for
is a diagnosis for
 w.r.t.
w.r.t.
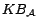 such that
such that
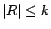 . (
. (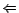 ) Suppose
) Suppose  is a diagnosis for
is a diagnosis for  w.r.t.
w.r.t.
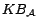 such that
such that
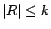 . It is not
hard to see that any set of assertions of the form
. It is not
hard to see that any set of assertions of the form
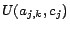 (
(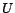 is either
is either 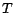 or
or 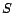 ) must have exactly
) must have exactly 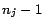 assertions in
assertions in  and one in
and one in
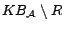 . To
see that
. To
see that 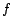 is satisfiable, for each
is satisfiable, for each
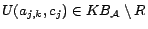 (
(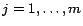 ), if
), if 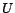 is
is 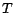 ,
we assign
,
we assign 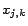 (i.e. the
corresponding variable of
(i.e. the
corresponding variable of 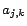 in
in 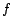 )
) 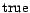 ; otherwise we assign
; otherwise we assign 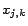
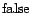 . The above
(partial) assignment on
. The above
(partial) assignment on
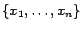 is consistent
and ensures
is consistent
and ensures
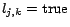 for all
for all
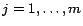 . Thus
. Thus 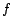 is satisfiable.
is satisfiable.
Since the construction of  is
accomplished in PTIME and the SAT problem is NP-complete, and
since
is
accomplished in PTIME and the SAT problem is NP-complete, and
since
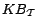 has a fixed size,
this theorem follows.
has a fixed size,
this theorem follows.
As analyzed in related work, a method that computes minimum
cost diagnoses based on minimal conflict sets is impractical,
because it may require both exponential time and exponential
space. We thus consider methods that need not compute minimal
conflict sets. A naive method is the black-box method, which
searches minimum cost diagnoses over all subsets of removal
assertions by applying a DL reasoner to check diagnoses. However,
the black-box method cannot compute a minimum cost diagnosis for
a DL-Lite ontology in polynomial calls to a DL reasoner,
otherwise a minimum cost diagnosis can be computed in PTIME
w.r.t. data complexity, contradicting Theorem 2. In order to find a
practical computational method, we consider transforming the
input ontology  into a positive program
into a positive program
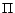 such that for any subset
such that for any subset
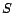 of
of 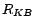 the set of removable assertions,
the set of removable assertions, 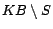 is consistent if and only if
is consistent if and only if
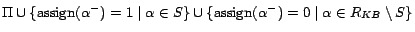 is satisfiable, where
is satisfiable, where 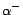 is a
fresh ground atom corresponding to ground atom
is a
fresh ground atom corresponding to ground atom 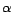 in
in 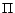 , and
, and
 denotes
the 0-1 truth value of
denotes
the 0-1 truth value of 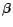 . Then, a
minimum cost diagnosis corresponds to a valuation of
. Then, a
minimum cost diagnosis corresponds to a valuation of  such that
such that
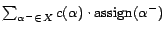 is minimum and
is minimum and 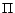 is satisfiable,
where
is satisfiable,
where
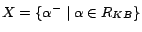 .
.
To find such a valuation of  , we
need to handle pseudo-boolean constraints (PB-constraints)
of the form
, we
need to handle pseudo-boolean constraints (PB-constraints)
of the form
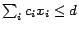 with
constants
with
constants
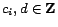 and
variables
and
variables 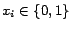 , or a linear
optimization function of the form minimize
, or a linear
optimization function of the form minimize
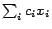 with constants
with constants
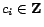 and variables
and variables
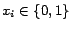 , where
, where 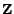 denotes the integer
domain. The SAT problems with PB-constraints and linear
optimization functions are well studied in the SAT community (cf.
http://www.cril.univ-artois.fr/PB07/). A SAT
problem with linear optimization functions can be translated into
a set of SAT problems with PB-constraints. A SAT problem with
PB-constraints can be either solved by standard SAT solvers after
translating PB-constraints to SAT clauses [5], or solved by extended SAT solvers
that support PB-constraints natively (e.g., PUEBLO [28]).
denotes the integer
domain. The SAT problems with PB-constraints and linear
optimization functions are well studied in the SAT community (cf.
http://www.cril.univ-artois.fr/PB07/). A SAT
problem with linear optimization functions can be translated into
a set of SAT problems with PB-constraints. A SAT problem with
PB-constraints can be either solved by standard SAT solvers after
translating PB-constraints to SAT clauses [5], or solved by extended SAT solvers
that support PB-constraints natively (e.g., PUEBLO [28]).
Now, the remaining problems are how to transform a
 ontology to the
intended positive program and how to efficiently compute minimum
cost diagnoses. We address these problems in the following
subsections.
ontology to the
intended positive program and how to efficiently compute minimum
cost diagnoses. We address these problems in the following
subsections.
Given a possibly inconsistent
 ontology
ontology
 , we first employ the KAON2
transformation method [12,21], described in Preliminaries, to
reduce
, we first employ the KAON2
transformation method [12,21], described in Preliminaries, to
reduce  to a disjunctive datalog
program
to a disjunctive datalog
program
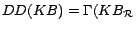 ,
,
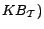
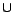
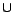
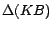 , but introduce a special treatment. The
original KAON2 transformation method allows equality atoms (of
the form
, but introduce a special treatment. The
original KAON2 transformation method allows equality atoms (of
the form 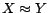 or
or 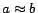 , where
, where 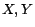 denote variables and
denote variables and 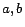 denote constants) to occur in rule bodies in
denote constants) to occur in rule bodies in
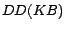 while disallows
inequality atoms (of the form
while disallows
inequality atoms (of the form
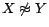 or
or
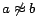 ) to occur in
) to occur in
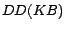 . To handle inequality
assertions in a similar way as other assertions, we first move
equality atoms (
. To handle inequality
assertions in a similar way as other assertions, we first move
equality atoms (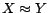 or
or
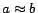 ) in any rule body in
) in any rule body in
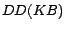 to the corresponding rule
head and replace them with inequality atoms (
to the corresponding rule
head and replace them with inequality atoms (
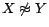 or
or
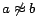 ), then append to
), then append to
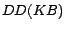 a constraint
a constraint
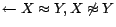 (written
(written
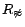 ), so that
), so that
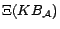 is simplified
to a direct translation from assertions in
is simplified
to a direct translation from assertions in
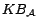 to ground facts in
to ground facts in
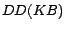 . Having such treatment we
simply denote
. Having such treatment we
simply denote
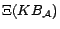 as
as
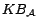 . The modified
rules in
. The modified
rules in 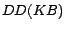 are still safe due to
the restricted form of the original rules that have equality
atoms in the body. In essence, our treatment views an inequality
atom as an ordinary one and does not impact the satisfiability of
are still safe due to
the restricted form of the original rules that have equality
atoms in the body. In essence, our treatment views an inequality
atom as an ordinary one and does not impact the satisfiability of
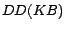 . Then, we convert
. Then, we convert
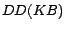 to a repair
program
to a repair
program
 defined below.
Intuitively, the decision atom
defined below.
Intuitively, the decision atom 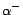 is introduced to weaken
is introduced to weaken  , so that
, so that
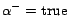 (resp.
(resp.
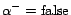 ) implies
that
) implies
that 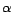 is removed from (resp.
kept in)
is removed from (resp.
kept in)  . Note that decision atoms
in
. Note that decision atoms
in
 are treated as
nullary ground atoms.
are treated as
nullary ground atoms.
Definition 2 For

a possibly inconsistent

ontology and
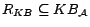
a set of removable assertions such that each assertion
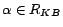
is given a
removal cost
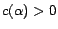
, a
repair program of

w.r.t.
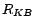
, written

, is a
disjunctive datalog program converted from
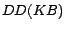
as follows: for each assertion
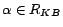
, we introduce
a corresponding
decision atom 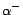
and give it a cost
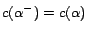
, then
replace the ground fact
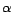
in
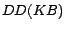
with
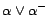
. We simply
call

a repair
program if
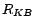
is clear from
the context.
Example 2
Let
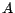
,
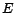
,
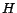
,

,
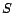
,
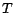
,
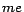
and
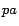
abbreviate
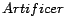
,
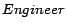
,
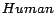
,
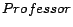
,
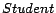
,
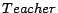
,
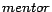
and
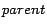
respectively. Given a

ontology
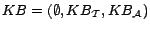
, where
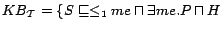
,
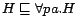
,
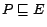
,
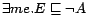
,
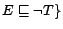
and
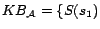
,
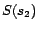
,
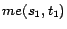
,
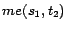
,
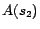
,
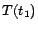
,
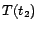
,
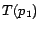
,
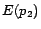
,
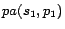
,
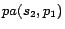
,
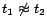
,
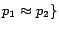
, and a set of
removable assertions
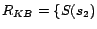
,
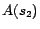
,
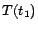
,
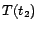
,
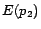
,
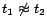
,
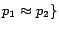
such that
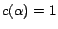
for each assertion
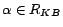
, we construct
the repair program

as follows.
First, by applying the KAON2 transformation method with our
special treatment, we reduce  to
to
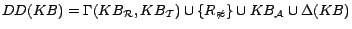 ,
where
,
where
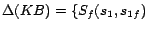 ,
,
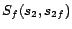 ,
,
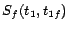 ,
,
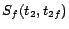 ,
,
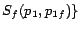 and
and
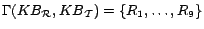 as given below.
as given below.
- R1:
-
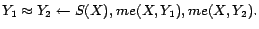
- R2:
-
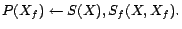
- R3:
-
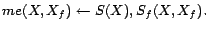
- R4:
-
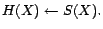
- R5:
-
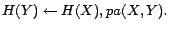
- R6:
-
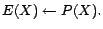
- R7:
-
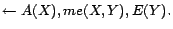
- R8:
-
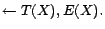
- R9:
-
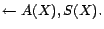
Then, by introducing decision atoms and converting ground
facts in 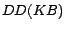 , we obtain
, we obtain
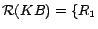 , ...,
, ...,
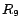 ,
,
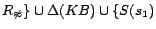 ,
,
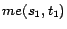 ,
, 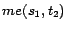 ,
, 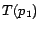 ,
, 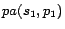 ,
,
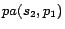 ,
,
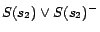 ,
,
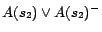 ,
,
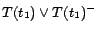 ,
,
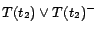 ,
,
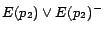 ,
,
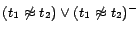 ,
,
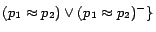 .
.
There exists a correspondence between minimum cost diagnoses
for  w.r.t.
w.r.t. 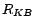 and
and  -MC models of
-MC models of
 , where
, where
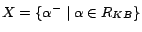 (see Theorem 3). A model
(see Theorem 3). A model 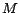 of a positive program
of a positive program  is called an
is called an  -MC model of
-MC model of
 if there is no model
if there is no model
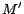 of
of  such that
such that
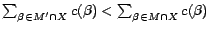 ,
where
,
where  is a set of ground atoms and
is a set of ground atoms and
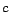 is a predefined cost function
over
is a predefined cost function
over  .
.
Proof sketch. (Soundness) Let 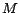 be an
be an  -MC model of
-MC model of
 ,
,
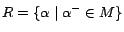 and
and
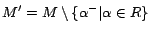 . It can be
shown that
. It can be
shown that 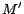 is a model of
is a model of
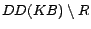 . By Theorem
1,
. By Theorem
1,  is diagnosis of
is diagnosis of  w.r.t.
w.r.t. 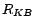 . Further,
. Further,
 must be a minimum cost
diagnoses, otherwise it can be shown that there exists a model
must be a minimum cost
diagnoses, otherwise it can be shown that there exists a model
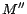 of
of
 s.t.
s.t.
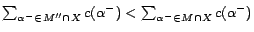 .
.
(Completeness) Let  be a minimum
cost diagnosis for
be a minimum
cost diagnosis for  w.r.t.
w.r.t.
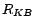 . By Theorem 1,
. By Theorem 1,
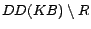 is satisfiable
and thus has a model, say
is satisfiable
and thus has a model, say 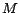 . It can
be shown that
. It can
be shown that
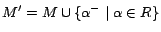 is a model of
is a model of
 . Further,
. Further,
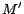 must be an
must be an  -MC model of
-MC model of
 , otherwise it
can be shown that there exists a diagnosis
, otherwise it
can be shown that there exists a diagnosis 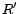 for
for  w.r.t.
w.r.t.
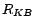 s.t.
s.t.
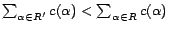 .
.
By Theorem 3, the
problem of finding minimum cost diagnoses for  w.r.t.
w.r.t. 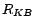 is reduced
to the problem of computing
is reduced
to the problem of computing  -MC
models of
-MC
models of
 , which can be
realized by applying SAT solvers. However, SAT solvers take a
positive propositional program as input and do not distinguish
equality atoms from other atoms. To treat the equality predicate
, which can be
realized by applying SAT solvers. However, SAT solvers take a
positive propositional program as input and do not distinguish
equality atoms from other atoms. To treat the equality predicate
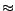 , which is interpreted as
a congruence relation, as an ordinary predicate, we use a
well-known transformation from [8]. For a disjunctive datalog program
, which is interpreted as
a congruence relation, as an ordinary predicate, we use a
well-known transformation from [8]. For a disjunctive datalog program
 , let
, let 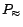 denote the program consisting of the rules
stating that the equality predicate is reflexive,
symmetric and transitive, and the replacement
rules given below, instantiated for each predicate
denote the program consisting of the rules
stating that the equality predicate is reflexive,
symmetric and transitive, and the replacement
rules given below, instantiated for each predicate
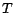 in
in  (excluding
(excluding 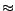 ) and each position
) and each position
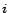 . Note that the reflexive rule
is not safe and is instead represented as a set of ground facts
of the form
. Note that the reflexive rule
is not safe and is instead represented as a set of ground facts
of the form 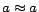 , instantiated for
each constant
, instantiated for
each constant 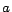 in
in  . Then, appending
. Then, appending 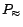 to
to  allows to treat
allows to treat
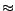 as an ordinary
predicate.
as an ordinary
predicate.
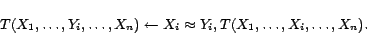
For the input issue, we need to ground
 before applying
SAT solvers. A well-known grounding technique is intelligent
grounding (IG) [7], which
only applies to equality-free disjunctive datalog programs. That
is, if the equality predicate
before applying
SAT solvers. A well-known grounding technique is intelligent
grounding (IG) [7], which
only applies to equality-free disjunctive datalog programs. That
is, if the equality predicate 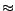 is present in a disjunctive datalog program
is present in a disjunctive datalog program  , we must append
, we must append 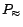 to
to  before grounding
before grounding
 using the IG technique. The IG
technique has been implemented in a disjunctive datalog engine
DLV [18], but the current
implementation cannot handle large disjunctive datalog programs
due to memory limitation1, especially when the equality
predicate is present. On the other hand, current implementations
of SAT solvers lack scalability for large propositional programs.
To address these problems, we develop two disk-based algorithms
for grounding
using the IG technique. The IG
technique has been implemented in a disjunctive datalog engine
DLV [18], but the current
implementation cannot handle large disjunctive datalog programs
due to memory limitation1, especially when the equality
predicate is present. On the other hand, current implementations
of SAT solvers lack scalability for large propositional programs.
To address these problems, we develop two disk-based algorithms
for grounding
 to
to 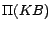 and for partitioning
and for partitioning
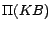 to disjoint subprograms
respectively, so that the computation of minimum cost diagnoses
can be separately performed over each subprogram.
to disjoint subprograms
respectively, so that the computation of minimum cost diagnoses
can be separately performed over each subprogram.
Algorithm 1 is our
algorithm for grounding a repair program  . By
. By 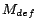 we denote the
unique minimal model of the definite fragment of
we denote the
unique minimal model of the definite fragment of
 , i.e.
, i.e.
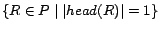 .
. 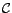 is actually the set of congruence classes
is actually the set of congruence classes
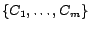 occurring in
occurring in
 , where
, where
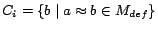 for an arbitrary
constant
for an arbitrary
constant 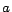 occurring in some equality
atom in
occurring in some equality
atom in 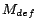 that is not of the
form
that is not of the
form 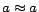 .
.
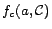 denotes the
congruence class in
denotes the
congruence class in 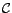 that
contains constant
that
contains constant 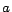 .
. 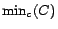 denotes the constant
denotes the constant 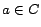 having the smallest value in
having the smallest value in
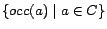 , where
, where
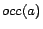 is the occurrence order
of
is the occurrence order
of 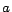 in
in  .
.
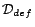 is actually a
set of non-equality atoms in
is actually a
set of non-equality atoms in 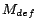 such that for each non-equality atom
such that for each non-equality atom
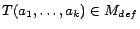 ,
there exists a unique ground atom
,
there exists a unique ground atom
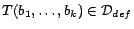 such that for each
such that for each
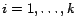 ,
, 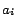 and
and 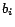 are either
the same or together in some
are either
the same or together in some
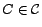 .
. 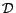 is the set of ground atoms occurring in
the grounded program
is the set of ground atoms occurring in
the grounded program 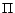 .
.
Let 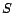 and
and 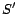 be two sets of ground atoms.
be two sets of ground atoms. 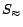 denotes the subset of
denotes the subset of 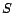 consisting of all equality atoms in
consisting of all equality atoms in 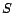 ;
;
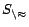 denotes
denotes
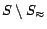 . For a rule
. For a rule
 , the function
GetSubstitutes(
, the function
GetSubstitutes( ,
,
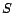 ,
, 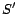 ) returns the set of all ground substitutes
) returns the set of all ground substitutes 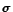 such that
such that 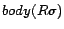
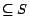 ,
,
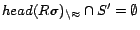 and
and
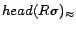 does not
contain equality atoms of the form
does not
contain equality atoms of the form 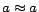 . The function Rewrite(
. The function Rewrite(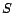 ,
, 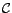 ) rewrites
all constants
) rewrites
all constants 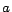 in
in 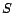 such that
such that
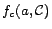 exists to
exists to
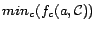 , and
returns the modified
, and
returns the modified 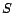 .
.
The algorithm consists of three steps. Step 1 (lines 1-13)
computes 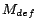 in a standard
iterative manner, but represents
in a standard
iterative manner, but represents 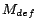 as
as
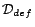 and
and
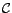 . Step 2 (lines
14-16) rewrites the constants occurring in disjunctive ground
facts (of the form
. Step 2 (lines
14-16) rewrites the constants occurring in disjunctive ground
facts (of the form
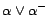 ) in
) in
 , because some constants
occurring in
, because some constants
occurring in 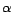 are represented
by other constants in step 1. At a word, in step 1 and step 2,
all constants in a congruence class are replaced with a same
constant, so as to reduce the number of instantiated rules in
step 3. Step 3 (lines 17-26) grounds
are represented
by other constants in step 1. At a word, in step 1 and step 2,
all constants in a congruence class are replaced with a same
constant, so as to reduce the number of instantiated rules in
step 3. Step 3 (lines 17-26) grounds 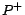 , i.e.
, i.e.
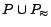 excluding the
definite ground facts, in a standard iterative manner based on
excluding the
definite ground facts, in a standard iterative manner based on
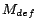 . Each instantiated rule
. Each instantiated rule
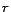 such that
such that
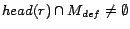 is ignored (line 22), because
is ignored (line 22), because 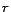 has no
impact on computing models of
has no
impact on computing models of  . If
. If
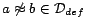 , the equality atom
, the equality atom
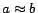 in an instantiated
rule head is not appended to
in an instantiated
rule head is not appended to 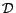 (line 24), because it cannot occur in any
model of
(line 24), because it cannot occur in any
model of  . The ground atoms in
. The ground atoms in
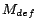 are removed from the
body of any instantiated rule (lines 25-26), because they are in
every model of
are removed from the
body of any instantiated rule (lines 25-26), because they are in
every model of  . Note that the function
GetSubstitutes can be realized by applying a SQL engine
and its results can be stored in disk, so the algorithm is
disk-based. In what follows, by
. Note that the function
GetSubstitutes can be realized by applying a SQL engine
and its results can be stored in disk, so the algorithm is
disk-based. In what follows, by 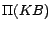 we denote the grounded repair program returned by
Ground(
we denote the grounded repair program returned by
Ground(
 ).
).
Example 3
Continue with Example
2. We now demonstrate how
Ground(

) works. In
step 1, we compute the unique minimal model
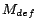
of
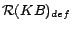
in an
iterative manner, obtaining
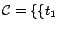
,
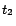
,
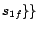
and
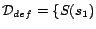
,
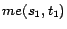
,
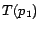
,
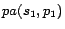
,
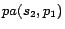
,
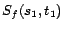
,
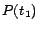
,
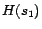
,
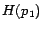
,
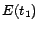
,
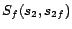
,
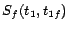
,
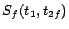
,
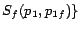
. In step 2,
according to
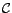
, we
replace the set of disjunctive ground facts in

with
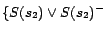
,
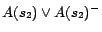
,
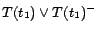
,
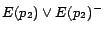
,
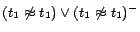
,
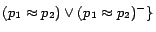
. In step 3, we
ground
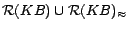
(excluding
the definite ground facts) in an iterative manner, obtaining a
propositional program
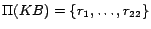
,
where
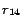
is instantiated
from
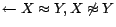
(i.e.
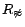
),
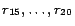
are
instantiated from
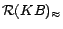
. Note
that for instantiating a rule that contains
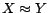
in the body, we only consider all ground
substitutes
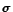
such that
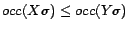
,
where
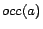
is the occurrence
order of constant
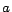
in

.
Algorithm 2 is our
algorithm for partitioning a positive propositional program
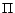 based on a set
based on a set  of ground atoms occurring in
of ground atoms occurring in
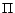 . The basic idea is to filter
out rules that have no impact on
. The basic idea is to filter
out rules that have no impact on 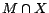 when constructing an
when constructing an  -MC model
-MC model 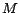 of
of
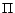 and put together remaining
rules that have common ground atoms to form disjoint subprograms.
In the algorithm, each ground atom
and put together remaining
rules that have common ground atoms to form disjoint subprograms.
In the algorithm, each ground atom 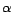 occurring in
occurring in 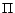 is
mapped to a partition identifier
is
mapped to a partition identifier 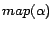 . For a rule
. For a rule 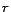 , we use
, we use
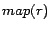 to denote
to denote
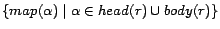 . To
simplify explanation, we call a rule
. To
simplify explanation, we call a rule 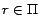 ready if
ready if
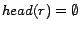 or
or 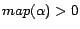 for all
for all
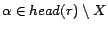 .
Before a ground atom is detected in some ready rule, it is mapped
to 0 (line 1). To process ready rules as early as possible,
constraints (which are ready rules) are moved in front of other
rules in
.
Before a ground atom is detected in some ready rule, it is mapped
to 0 (line 1). To process ready rules as early as possible,
constraints (which are ready rules) are moved in front of other
rules in 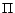 (line 2). Then,
(line 2). Then,
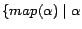 occurs
in
occurs
in 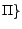 is adjusted in an
iterative manner until
is adjusted in an
iterative manner until
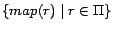 reaches a
fixpoint (lines 3-11). Each ground atom
reaches a
fixpoint (lines 3-11). Each ground atom 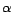 first detected in ready rules is initially mapped
to a unique partition identifer (lines 6-7). All ground atoms in
a ready rule
first detected in ready rules is initially mapped
to a unique partition identifer (lines 6-7). All ground atoms in
a ready rule 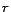 are mapped to the same
partition identifier (lines 8-10). After the loop is finished,
all ready rules in
are mapped to the same
partition identifier (lines 8-10). After the loop is finished,
all ready rules in 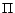 mapped to the
same partition identifier are put together, yielding a set of
nonempty subprograms
mapped to the
same partition identifier are put together, yielding a set of
nonempty subprograms
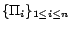 (lines
12-13).
(lines
12-13).
It can be seen that the number of iterations (lines 3-11) is
at most 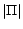 , because the
mapping adjustment (lines 9-10) ensures that in each iteration, a
ready rule
, because the
mapping adjustment (lines 9-10) ensures that in each iteration, a
ready rule 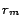 having the smallest
value of
having the smallest
value of 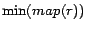 among
among
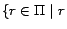 is ready and
is ready and
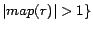 must
reach a state that
must
reach a state that 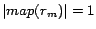 and that
and that 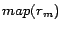 is unchanged in subsequent iterations.
Furthermore,
is unchanged in subsequent iterations.
Furthermore,
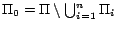 is the intended
set of filtered rules (see Lemma 1);
is the intended
set of filtered rules (see Lemma 1); 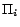 and
and 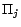 contain no
common ground atoms for all
contain no
common ground atoms for all
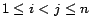 . Since
. Since
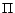 is sequentially accessed in
each iteration, the algorithm is also disk-based.
is sequentially accessed in
each iteration, the algorithm is also disk-based.
Lemma 1
Let
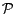
be the set of
subprograms returned by
Partition(
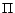
,

) and
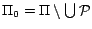
. For any

-MC model
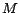
of
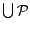
,
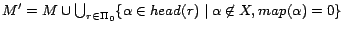
is an

-MC model of
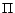
such that
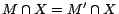
.
Proof. Let
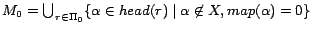 .
Since
.
Since
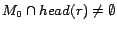 for every
for every 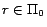 ,
, 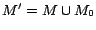 satisfies every rule in
satisfies every rule in 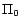 . Moreover, since
. Moreover, since 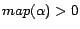 for every ground atom
for every ground atom 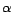 occurring in
occurring in
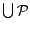 ,
,
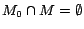 and thus
and thus
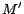 still satisfies every rule in
still satisfies every rule in
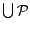 as
as
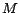 . It follows that
. It follows that 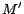 is a model of
is a model of 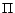 . Since
. Since
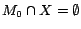 ,
, 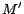 is an
is an  -MC model of
-MC model of 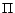 such that
such that
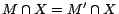 .
.
Example 4
Continue with Example
3. Let
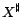
be the set of ground atoms of the form
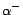
in
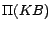
. We now demonstrate how
Partition(
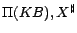
) works. We
first move
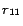
, ...,
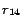
,
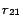
,
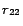
in front
of other rules in
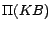
, then
map each ground atom in
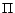
to
a partition identifier. In the first iteration for processing
rules
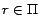
,
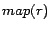
is set as follows (for every ground atom
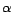
,
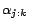
denotes
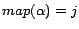
before processing
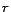
at line 8 in Algorithm
2, and
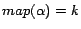
after the first iteration).
In the second iteration, it is detected that
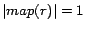
for all ready rules
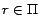
, so the loop is
finished. Finally we obtain four disjoint subprograms from the
resulting mapping:
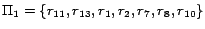
,
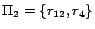
,
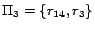
and
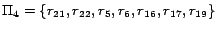
.
In what follows, we call a ground atom of the form 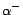 a translated
decision atom. Let
a translated
decision atom. Let 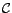 be
the set of congruence classes returned by Ground(
be
the set of congruence classes returned by Ground(
 ), and
), and
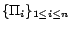 the
set of subprograms returned by Partition(
the
set of subprograms returned by Partition(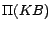 ,
, 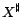 ), where
), where
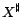 is the set of
translated decision atoms occurring in
is the set of
translated decision atoms occurring in 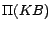 . We intend to compute
. We intend to compute  -MC models of
-MC models of
 over each of
over each of
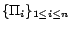 , where
, where
 is the set of decision atoms
occurring in
is the set of decision atoms
occurring in
 . However, some
decision atoms are replaced with other atoms in
. However, some
decision atoms are replaced with other atoms in
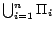 , because
all constants in a congruence class in
, because
all constants in a congruence class in 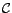 are replaced with a same constant. Let
are replaced with a same constant. Let
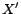 be the set of translated
decision atoms occurring in
be the set of translated
decision atoms occurring in
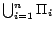 .
.
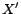 is said to be soundly
converted from
is said to be soundly
converted from  w.r.t.
w.r.t.
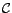 if each ground atom
if each ground atom
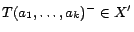 has
been given a cost
has
been given a cost
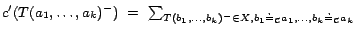
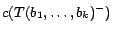 , where
, where
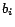
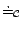
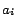 means that constants
means that constants
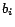 and
and 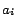 are the same or together in some
are the same or together in some
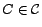 . Such conversion
is reasonable because all decision atoms
. Such conversion
is reasonable because all decision atoms
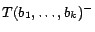
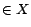 such that
such that
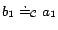 , ...,
, ...,
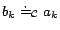 for
some
for
some
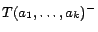
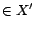 must be present or absent
together in every model of
must be present or absent
together in every model of
 . Moreover, given
a subset
. Moreover, given
a subset 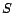 of
of 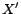 , we define a decoding of
, we define a decoding of 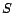 w.r.t.
w.r.t.  and
and 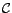 , written
, written
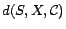 , as
, as
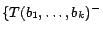
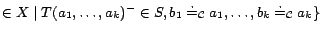 .
Then, a minimum cost diagnosis of
.
Then, a minimum cost diagnosis of  corresponds to a disjoint union of models in each subprogram (see
Theorem 4).
corresponds to a disjoint union of models in each subprogram (see
Theorem 4).
Example 5
Continue with Example
4. Let

be the set of decision atoms in

. In
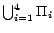
, the set
of ground atoms soundly converted from

w.r.t.
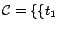
,
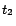
,
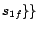
is
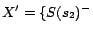
,
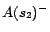
,
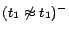
,
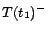
,
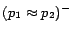
,
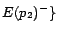
, where each ground
atom
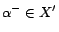
is given a cost
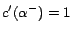
except that
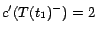
. Let
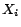
(
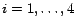
) be the subsets of
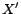
that occur in
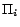
.
It is easy to see that
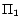
has two
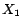
-MC models
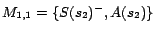
and
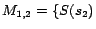
,
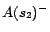
,
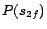
,
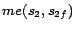
,
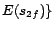
;
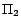
has a unique
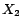
-MC model
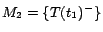
;
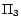
has a unique
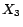
-MC model
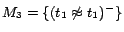
;
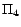
has two
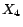
-MC models
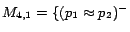
,
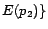
and
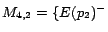
,
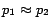
,
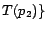
. Hence,
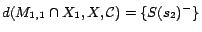
;
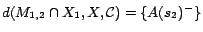
;
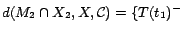
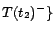
;
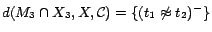
;
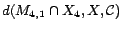
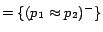
;
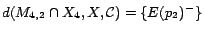
. By
Theorem
4, we
obtain four minimum cost diagnoses for

w.r.t.
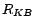
:
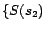
,
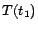
,
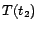
,
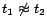
,
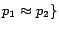
,
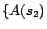
,
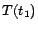
,
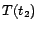
,
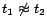
,
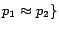
,
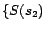
,
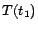
,
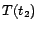
,
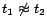
,
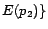
and
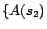
,
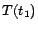
,
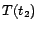
,
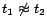
,
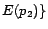
.
Proof sketch. (Soundness) For 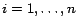 , let
, let 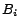 be
the set of ground atoms occurring in
be
the set of ground atoms occurring in 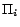 and
and 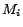 an
an
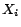 -MC model of
-MC model of 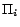 . Let
. Let
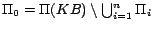 and
and
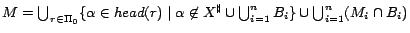 .
Let
.
Let 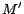 be the set of ground atoms
derived by applying all rules in
be the set of ground atoms
derived by applying all rules in
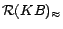 over
over
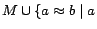 and
and
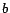 are together in some
are together in some
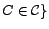 , and
, and
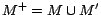 . It can be seen
that
. It can be seen
that
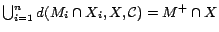 . It
can further be shown that
. It
can further be shown that 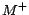 is
an
is
an  -MC model of
-MC model of
 . By Theorem
3,
. By Theorem
3,
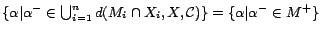 is a minimum cost diagnosis for
is a minimum cost diagnosis for  w.r.t.
w.r.t. 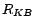 .
.
(Completeness) Let  be a minimum
cost diagnosis for
be a minimum
cost diagnosis for  w.r.t.
w.r.t.
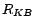 . By Theorem 3, there exists an
. By Theorem 3, there exists an  -MC model
-MC model 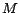 of
of
 s.t.
s.t.
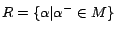 .
Let
.
Let 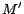 be a set of ground atoms
converted from
be a set of ground atoms
converted from 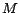 by rewriting each
constant
by rewriting each
constant 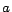 in
in 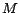 s.t.
s.t.
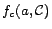 exists to
exists to
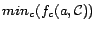 . It
can be shown that
. It
can be shown that
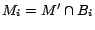 is an
is an 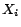 -MC model of
-MC model of 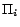 (
(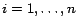 )
s.t.
)
s.t.
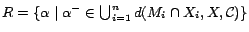 .
.
By Theorem 4,
the problem of finding minimum cost diagnoses for  w.r.t.
w.r.t. 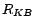 is reduced
to
is reduced
to 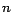 subproblems, each of which
computes
subproblems, each of which
computes 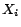 -MC models of
-MC models of 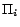 (
(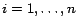 ). We consider computing
). We consider computing 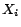 -MC models of
-MC models of 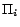 by
applying SAT solvers that support PB-constraints. We assume that
the cost of each atom in
by
applying SAT solvers that support PB-constraints. We assume that
the cost of each atom in 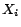 has
been scaled to a positive integer polynomial in
has
been scaled to a positive integer polynomial in 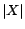 the total number of removable assertions.
Then, the first
the total number of removable assertions.
Then, the first 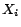 -MC model of
-MC model of
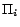 can be computed by a
binary search (within range
can be computed by a
binary search (within range
![$[0,\sum_{\beta\in X_i}c'(\beta)]$](fp226-du-img523.gif) ) for the minimum value
) for the minimum value
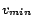 such that
such that
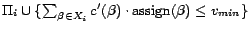 is satisfiable, taking
is satisfiable, taking
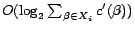
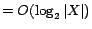 calls to
a SAT solver. Let
calls to
a SAT solver. Let
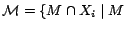 is
a previously computed
is
a previously computed 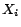 -MC model of
-MC model of
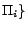 . Then a next
. Then a next 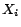 -MC model
-MC model 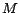 of
of 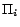 , such that
, such that
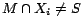 for every
for every
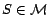 , can be computed
as a model of
, can be computed
as a model of
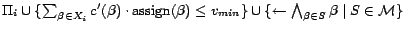 ,
by calling a SAT solver once.
,
by calling a SAT solver once.
Consider the time complexity for computing minimum cost
diagnoses. Under the data complexity assumption, the number of
non-ground rules in
 and the number
of different variables in each rule in
and the number
of different variables in each rule in
 are bounded by
constants. Thus the number of rules in
are bounded by
constants. Thus the number of rules in 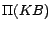 is polynomial in
is polynomial in
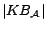 . It
follows that Ground(
. It
follows that Ground(
 ) is executed in
PTIME. Let
) is executed in
PTIME. Let 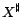 be the set of
translated decision atoms occurring in
be the set of
translated decision atoms occurring in 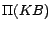 . Partition(
. Partition(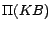 ,
, 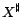 ) commits
at most
) commits
at most 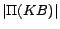 iterations
over
iterations
over 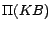 , so it is executed in
PTIME too. Let
, so it is executed in
PTIME too. Let 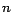 be the number of
removable assertions in
be the number of
removable assertions in  and
and
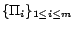 be the
set of propositional programs returned by
Partition(
be the
set of propositional programs returned by
Partition(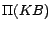 ,
,
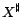 ). Note that the SAT
problem with a PB-constraint is NP-complete. Since
). Note that the SAT
problem with a PB-constraint is NP-complete. Since 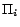 and
and 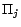 have no common ground atoms for all
have no common ground atoms for all
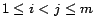 ,
, 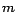 calls to a SAT solver over
calls to a SAT solver over
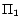 , ...,
, ..., 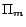 respectively amount to one call to an NP oracle
over
respectively amount to one call to an NP oracle
over
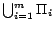 . Under the
assumption that each removal cost has been scaled to a positive
integer polynomial in
. Under the
assumption that each removal cost has been scaled to a positive
integer polynomial in 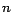 , it follows from
Theorem 4 that, the
first minimum cost diagnosis is computed in
, it follows from
Theorem 4 that, the
first minimum cost diagnosis is computed in 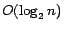 calls to an NP oracle, and a next one, in
one more call.
calls to an NP oracle, and a next one, in
one more call.
We implemented the proposed method for computing minimum cost
diagnoses in GNU C++. In the implementation, MySQL is used as the
back-end SQL engine; ABox assertions and new ground atoms derived
in the grounding process are maintained in a SQL database; All
ground substitutes of rules, retrieved via SQL statements, are
maintained in disk files; The SAT solver MiniSat [5], which
supports PB-constraints and linear optimization functions by
internally translating them into SAT clauses, is applied to
compute
[5], which
supports PB-constraints and linear optimization functions by
internally translating them into SAT clauses, is applied to
compute  -MC models. All the
experiments were conducted on a 3.2GHz Pentium 4 CPU 2GB RAM PC
running Windows XP and Cygwin.
-MC models. All the
experiments were conducted on a 3.2GHz Pentium 4 CPU 2GB RAM PC
running Windows XP and Cygwin.
Semintec2is an ontology about financial
services, created in the SEMINTEC project at the University of
Poznan. Its intensional part contains functional roles and
disjointness constraints.
HumanCyc3 is an ontology on human metabolic
pathways and human genome, created by the SRI International
corporation. Since its intensional part contains nomimals and
concrete domain specifications (e.g., a role range is of some
datatype, a concrete role is functional, etc.) that cannot be
handled by our method, we converted nominals to new atomic
concepts and deleted concrete domain specifications. The weakened
intensional part still contains disjunctions, functional
roles/restrictions and disjointness constraints.
LUBM4 is a benchmark ontology developed
at the Lehigh University [9].
Since its intensional part has no functional roles, number
restrictions or disjointness constraints, which implies that it
cannot be inconsistent, we extended it by adding a functional
role headOf and an inverse functional role
isTaughtBy, where headOf (resp.
isTaughtBy) is also defined as an inverse role of
isHeadOf (resp. teacherOf), and adding
disjointness constraints
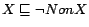 for each
existing concept name
for each
existing concept name  , where
, where
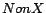 is a new concept name. LUBM
comes with an ABox generator. Let LUBM
is a new concept name. LUBM
comes with an ABox generator. Let LUBM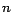 denote the ontology obtained from the generator by setting the
number of universities to
denote the ontology obtained from the generator by setting the
number of universities to 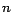 .
.
Before testing the proposed method, the intensional parts of
the above ontologies were offline transformed to datalog programs
using the KAON2 DL reasoner5. Each transformation was
performed in less than one second. Moreover, ABox assertions of
the above ontologies were stored into MySQL databases, where
duplicated ABox assertions were removed. Table 1 summarizes the complexity of
the test ontologies and the datalog programs transformed from
their intensional parts, where HumanCyc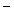 denotes the weakened HumanCyc, and LUBM
denotes the weakened HumanCyc, and LUBM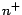 denotes the extended LUBM
denotes the extended LUBM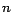 .
.
Table 1:
The complexity of test ontologies
| |
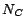 |
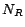 |
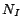 |
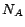 |
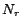 |
Features |
| S |
59 |
16 |
17,941 |
65,291 |
221 |
EQ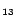 ,DS ,DS |
| H |
27 |
49 |
82,095 |
154,110 |
159 |
EQ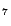 ,DS ,DS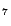 |
| L1 |
86 |
34 |
50,253 |
120,274 |
168 |
EQ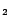 ,DS ,DS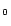 |
| L10 |
86 |
34 |
629,568 |
1,293,286 |
168 |
EQ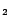 ,DS ,DS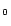 |
Note: S stands for Semintec. H stands for HumanCyc . L1 stands for
LUBM
. L1 stands for
LUBM . L10 stands for
LUBM
. L10 stands for
LUBM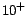 .
. 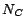 is the number of concept names.
is the number of concept names. 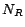 is the number of role names.
is the number of role names. 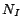 is the number of individuals.
is the number of individuals. 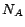 is the number of ABox assertions stored in MySQL
databases.
is the number of ABox assertions stored in MySQL
databases. 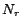 is the number of
rules transformed from the intensional part. The features show
how many special transformed rules: EQ
is the number of
rules transformed from the intensional part. The features show
how many special transformed rules: EQ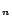 means there are
means there are 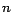 equality rules (i.e. rules containing equality atoms);
DS
equality rules (i.e. rules containing equality atoms);
DS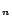 means there are
means there are 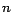 disjunctive rules.
disjunctive rules.
We developed a tool, called Injector, to inject a
given number of conflicts into an ontology. Given a consistent
ontology  and a number
and a number 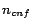 of conflicts to be
injected, Injector first deduces into
of conflicts to be
injected, Injector first deduces into  all atomic concept assertions that are consequences
of
all atomic concept assertions that are consequences
of  , then injects
, then injects 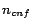 conflicts one by one. Let
conflicts one by one. Let 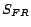 denote the set of functional/inverse functional
roles,
denote the set of functional/inverse functional
roles, 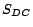 denote the set of atomic
concepts that have disjoint concepts. To inject a conflict,
Injector randomly selects an entity in
denote the set of atomic
concepts that have disjoint concepts. To inject a conflict,
Injector randomly selects an entity in
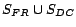 . In case an
functional role
. In case an
functional role  is selected, if
there exist role assertions over
is selected, if
there exist role assertions over  in
in  , Injector randomly
selects one, say
, Injector randomly
selects one, say 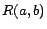 , and
appends
, and
appends 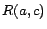 and
and
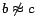 to
to  , where
, where 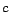 is a new individual; otherwise, Injector
appends
is a new individual; otherwise, Injector
appends 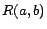 ,
, 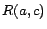 and
and
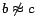 to
to  , where
, where 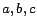 are new individuals. In case an inverse functional
role
are new individuals. In case an inverse functional
role  is selected, Injector
treats it as
is selected, Injector
treats it as 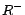 . In case an atomic
concept
. In case an atomic
concept 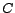 is selected, if there exist
concept assertions over
is selected, if there exist
concept assertions over 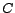 in
in
 , Injector randomly
selects one, say
, Injector randomly
selects one, say 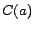 , and appends
, and appends
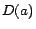 to
to  for a randomly selected disjoint concept
for a randomly selected disjoint concept 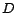 of
of 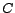 ;
otherwise, Injector appends
;
otherwise, Injector appends 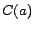 and
and 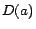 to
to
 , where
, where 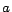 is a new individual and
is a new individual and 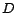 a
randomly selected disjoint concept of
a
randomly selected disjoint concept of 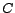 .
Injector was implemented in JAVA, using the Pellet
[29] API to deduce all atomic
concept assertions that are consequences of a consistent
ontology.
.
Injector was implemented in JAVA, using the Pellet
[29] API to deduce all atomic
concept assertions that are consequences of a consistent
ontology.
We injected different number of conflicts to the four test
ontologies using Injector, obtaining a set of
inconsistent ontologies. We consider the hardest case where all
assertions in an obtained ontology are assumed removable. We
assume that each assertion is given a removal cost 1. In order to
make the implemented system terminate in an acceptable time, we
set a time limit of 20 minutes for one call to MiniSat .
.
The test results are reported in Table 2. In each block, the first row
lists 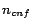 , i.e. the number of
injected conflicts; the second row lists the total execution time
for computing the first minimum cost diagnosis, starting from
transforming the input ontology. For Semintec and
HumanCyc
, i.e. the number of
injected conflicts; the second row lists the total execution time
for computing the first minimum cost diagnosis, starting from
transforming the input ontology. For Semintec and
HumanCyc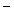 , the implemented system
cannot handle more injected conflicts in our test environment,
because when
, the implemented system
cannot handle more injected conflicts in our test environment,
because when 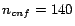 for Semintec
(or
for Semintec
(or 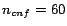 for
HumanCyc
for
HumanCyc ), some call to
MiniSat
), some call to
MiniSat exceeds the time limit. In
contrast, the implemented system scales well on LUBM
exceeds the time limit. In
contrast, the implemented system scales well on LUBM /LUBM
/LUBM ontologies with increasing number (from 1000) of
conflicts.
ontologies with increasing number (from 1000) of
conflicts.
We also collected runtime statistics on the partitioning
process. Let  be an inconsistent
ontology reported in Table 2. As can be seen, the number of
rules in each grounded repair program
be an inconsistent
ontology reported in Table 2. As can be seen, the number of
rules in each grounded repair program 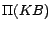 is up to millions. In addition, the number of
decision atoms in
is up to millions. In addition, the number of
decision atoms in 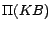 is at
least in thousands. We experimentally verified that any
is at
least in thousands. We experimentally verified that any
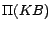 , without being
partitioned, cannot be handled by MiniSat
, without being
partitioned, cannot be handled by MiniSat because the execution exceeds the time or memory limit.
This shows the importance of the partitioning process.
because the execution exceeds the time or memory limit.
This shows the importance of the partitioning process.
Other statistics show the effectiveness of the partitioning
process. The percentage of filtered rules,
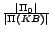 , is at least 11%
for all reported ontologies (esp., at least 57% for
LUBM
, is at least 11%
for all reported ontologies (esp., at least 57% for
LUBM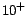 ontologies). The number of
disjoint subprograms of
ontologies). The number of
disjoint subprograms of 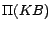 (i.e. the number of partitions),
(i.e. the number of partitions), 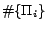 , increases when the number of
conflicts increases. This shows that the partitioning process
improves the scalability.
, increases when the number of
conflicts increases. This shows that the partitioning process
improves the scalability.
Table 2 also reports
the maximum number of ground rules in each partition,
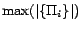 , and
the maximum number of translated decision atoms in each
partition,
, and
the maximum number of translated decision atoms in each
partition,
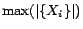 . It can
be seen that the total execution time is roughly dominated by
. It can
be seen that the total execution time is roughly dominated by
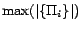 and
and
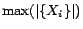 . For
Semintec and HumanCyc
. For
Semintec and HumanCyc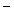 , since
, since
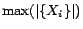 is up to
tens of thousands, the execution of MiniSat
is up to
tens of thousands, the execution of MiniSat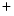 over the largest partition quickly exceeds the time
limit when the number of conflicts increases (as
over the largest partition quickly exceeds the time
limit when the number of conflicts increases (as
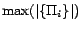 increases too). In contrast, for LUBM
increases too). In contrast, for LUBM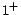 and LUBM
and LUBM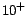 , since
, since
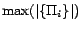 or
or
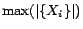 is
stable around a relatively small value, the total execution time
increases smoothly when the number of conflicts increases.
is
stable around a relatively small value, the total execution time
increases smoothly when the number of conflicts increases.
We can conclude that the performance of our method depends on
the effectiveness of the partitioning process. As for what
influences such effectiveness when the number of assertions and
the number of conflicts are fixed, we can see from Table 1 and Table 2 that, equality rules have a
stronger impact than normal rules; further, disjunctive rules
have a stronger impact than equality rules. Hence, we believe
that our method can handle any real (populated) ontology that has
up to millions of assertions together with a moderately complex
intensional part, which can be transformed to up to hundreds of
datalog rules with a few disjunctive rules and equality
rules.
A DL-based ontology may become inconsistent after it is
populated. In this paper, we proposed a solution to repair the
populated ontology by deleting assertions in a minimum cost
diagnosis. We first showed the intractability of finding a
minimum cost diagnosis, then presented an exact method for
computing minimum cost diagnoses for
 ontologies. The
method transforms a
ontologies. The
method transforms a
 ontology to a set
of disjoint propositional programs in PTIME w.r.t. data
complexity, thus reducing the original problem into a set of
independent subproblems. Each such subproblem computes an
ontology to a set
of disjoint propositional programs in PTIME w.r.t. data
complexity, thus reducing the original problem into a set of
independent subproblems. Each such subproblem computes an
 -MC model and is solvable by
applying SAT solvers. We experimentally showed that the method
can handle moderately complex ontologies with over thousands of
assertions, where all assertions can be assumed removable.
Especially, the method scales well on the extended LUBM
ontologies with increasing number (from 1000) of conflicts.
-MC model and is solvable by
applying SAT solvers. We experimentally showed that the method
can handle moderately complex ontologies with over thousands of
assertions, where all assertions can be assumed removable.
Especially, the method scales well on the extended LUBM
ontologies with increasing number (from 1000) of conflicts.
For future work, we plan to enhance our method to cope with
concrete domain specifications, seek feasible approaches to
handling nomimals, and work on tractable approximate methods for
computing minimum cost diagnoses.
This
work is supported in part by NSFC grants 60673103, 60721061 and
60373052.
REFERENCES
[1]
F. Baader, D. Calvanese, D. L. McGuinness, D. Nardi, and P.
F. Patel-Schneider, editors.
The Description Logic Handbook: Theory, Implementation, and
Applications.
Cambridge University Press, 2003.
[2]
D. Calvanese, G. D. Giacomo, D. Lembo, M. Lenzerini, and R.
Rosati.
Dl-lite: Tractable description logics for ontologies.
In Proc. of AAAI'05, pages 602-607, 2005.
[3]
P. Cimiano and J. Volker.
Text2onto - a framework for ontology learning and data-driven
change discovery.
In Proc. of NLDB'05, pages 227-238, 2005.
[4]
J. Dolby, J. Fan, A. Fokoue, A. Kalyanpur, A. Kershenbaum,
L. Ma, J. W. Murdock, K. Srinivas, and C. A. Welty.
Scalable cleanup of information extraction data using
ontologies.
In Proc. of ISWC'07, pages 100-113, 2007.
[5]
N. Een and N. Sorensson.
Translating pseudo-boolean constraints into sat.
JSAT, 2:1-26, 2006.
[6]
T. Eiter, G. Gottlob, and H. Mannila.
Disjunctive datalog.
ACM Trans. Database Systems, 22(3):364-418, 1997.
[7]
T. Eiter, N. Leone, C. Mateis, G. Pfeifer, and F.
Scarcello.
A deductive system for non-monotonic reasoning.
In Proc. of LPNMR'97, pages 364-375, 1997.
[8]
M. Fitting.
First-order Logic and Automated Theorem Proving (2nd
ed.).
Springer-Verlag New York, Inc., Secaucus, NJ, USA, 1996.
[9]
Y. Guo, Z. Pan, and J. Heflin.
Lubm: A benchmark for owl knowledge base systems.
J. Web Sem., 3(2-3):158-182, 2005.
[10]
I. Horrocks, U. Sattler, and S. Tobies.
Practical reasoning for very expressive description
logics.
Logic Journal of the IGPL, 8(3), 2000.
[11]
Z. Huang, F. van Harmelen, and A. ten Teije.
Reasoning with inconsistent ontologies.
In Proc. of IJCAI'05, pages 454-459, 2005.
[12]
U. Hustadt, B. Motik, and U. Sattler.
Reducing
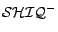 description
logic to disjunctive datalog programs.
description
logic to disjunctive datalog programs.
In Proc. of KR'04, pages 152-162, 2004.
[13]
A. Kalyanpur, B. Parsia, E. Sirin, and B. C. Grau.
Repairing unsatisfiable concepts in owl ontologies.
In Proc. of ESWC'06, pages 170-184, 2006.
[14]
A. Kalyanpur, B. Parsia, E. Sirin, and J. Hendler.
Debugging unsatisfiable classes in owl ontologies.
J. Web Sem., 3(4):268-293, 2005.
[15]
R. M. Karp.
Reducibility among combinatorial problems.
In Proc. of a Symposium on the Complexity of Computer
Computations, pages 85-103, 1972.
[16]
S. C. Lam, J. Z. Pan, D. H. Sleeman, and W. W.
Vasconcelos.
A fine-grained approach to resolving unsatisfiable
ontologies.
In Proc. of WI'06, pages 428-434, 2006.
[17]
D. Lembo and M. Ruzzi.
Consistent query answering over description logic
ontologies.
In Proc. of RR'07, pages 194-208, 2007.
[18]
N. Leone, G. Pfeifer, W. Faber, T. Eiter, G. Gottlob, S.
Perri, and F. Scarcello.
The dlv system for knowledge representation and
reasoning.
ACM Trans. Comput. Log., 7(3):499-562, 2006.
[19]
T. Meyer, K. Lee, and R. Booth.
Knowledge integration for description logics.
In Proc. of AAAI'05, pages 645-650, 2005.
[20]
T. Meyer, K. Lee, R. Booth, and J. Z. Pan.
Finding maximally satisfiable terminologies for the description
logic  .
.
In Proc. of AAAI'06, pages 269-274, 2006.
[21]
B. Motik.
Reasoning in Description Logics using Resolution and
Deductive Databases.
PhD thesis, Univesitat karlsruhe, Germany, Jan. 2006.
[22]
P. F. Patel-Schneider, P. Hayes, and I. Horrocks.
OWL Web Ontology Language Semantics and Abstract
Syntax.
W3C Recommendation, 2004.
http://www.w3.org/TR/owl-semantics/.
[23]
G. Qi, W. Liu, and D. A. Bell.
Knowledge base revision in description logics.
In Proc. of JELIA'06, pages 386-398, 2006.
[24]
R. Reiter.
A theory of diagnosis from first principles.
Artif. Intell., 32(1):57-95, 1987.
[25]
S. Schlobach.
Debugging and semantic clarification by pinpointing.
In Proc. of ESWC'05, pages 226-240, 2005.
[26]
S. Schlobach.
Diagnosing terminologies.
In Proc. of AAAI'05, pages 670-675, 2005.
[27]
S. Schlobach and R. Cornet.
Non-standard reasoning services for the debugging of
description logic terminologies.
In Proc. of IJCAI'03, pages 355-362, 2003.
[28]
H. M. Sheini and K. A. Sakallah.
Pueblo: A hybrid pseudo-boolean sat solver.
JSAT, 2:157-181, 2006.
[29]
E. Sirin, B. Parsia, B. C. Grau, A. Kalyanpur, and Y.
Katz.
Pellet: A practical owl-dl reasoner.
J. Web Sem., 5(2):51-53, 2007.
[30]
C. Welty and J. W. Murdock.
Towards knowledge acquisition from information
extraction.
In Proc. of ISWC'06, pages 152-162, 2006.
![]() ) ontologies. It
transforms a
) ontologies. It
transforms a
![]() ontology to a set
of disjoint propositional programs, thus reducing the original
problem into a set of independent subproblems. Each such
subproblem computes an optimal model and is solvable in
logarithmic calls to a SAT solver. Experimental results show
that the method can handle moderately complex ontologies with
over thousands of ABox assertions, where all ABox assertions
can be assumed removable.
ontology to a set
of disjoint propositional programs, thus reducing the original
problem into a set of independent subproblems. Each such
subproblem computes an optimal model and is solvable in
logarithmic calls to a SAT solver. Experimental results show
that the method can handle moderately complex ontologies with
over thousands of ABox assertions, where all ABox assertions
can be assumed removable.